- ... reālo1.1
- [vidusl. lat.
realis priekšmetisks, vielisks] - īstenībā esošs, patiess,
īstens.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... aksiomām1.2
- [gr. axioma] - pamattēze, kas ir
pamatā citu tēžu (teorēmu) pierādījumiem, attiecīgās zinātnes
teorijas ietvaros aksiomu pieņem bez pierādījuma.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Dedekinda1.3
- Šo
aksiomu pirmo reizi formulēja vācu matemātiķis R. Dedekinds (1831-1916)
savā darbā ``Nepārtrauktība un iracionālie skaitļi'' (publicēts 1872. g.).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
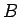 1.4
1.4
- Visiem
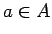 un visiem
un visiem
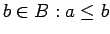 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... kopas1.5
- Visiem
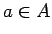 un visiem
un visiem
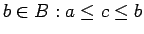 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Ģeometrijā1.6
- [gr. ge
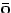 metria zemes mērīšana] -
matemātikas nozare, kas pētī gan telpas formas, gan ķermeņu
attiecības.
metria zemes mērīšana] -
matemātikas nozare, kas pētī gan telpas formas, gan ķermeņu
attiecības.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
taisnes1.7
- Taisne ar izvēlētu uz tās mērogu
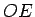 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... taisni1.8
- Jāievēro, ka koordinātu taišņu ir
bezgalīgi daudz, bet skaitļu taisne ir viena - reālo skaitļu
kopa.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...1.1. definīcija. 1.9
- [lat. definitio noteikšana] - jēdziena loģiska noteikšana.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... moduli1.10
- [lat. modulus mērs] -
šo skaitli attēlojošā vektora garums.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... indukcijas1.11
- [lat. inductio uzvedināšana] -
1) loģisks slēdziens no atsevišķiem gadījumiem uz vispārīgu
secinājumu;
2) mat. matemātiska pierādījuma paņēmiens,
kas pamatots uz pāreju no kādam naturālam skaitlim  pareiza secinājuma uz secinājumu, kas pareizs skaitlim
pareiza secinājuma uz secinājumu, kas pareizs skaitlim 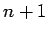 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... naturālo1.12
- [lat.naturalis] - dabisks, tāds,
kas nav mākslīgs.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... infīms1.13
- [lat.
infimum] -viszemākais
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... suprems1.14
- [lat.
supremum] - visaugstākais
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
1.1. teorēma. ]1.15
- [gr. the
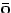 rēma apskatu, apdomāju]
apgalvojums, ko pierāda, balstoties vai nu uz aksiomām,
vai uz iepriekš pierādītiem apgalvojumiem.
rēma apskatu, apdomāju]
apgalvojums, ko pierāda, balstoties vai nu uz aksiomām,
vai uz iepriekš pierādītiem apgalvojumiem.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (skat.1.16
- Līdzīgi kā iepriekš
var definēt kopas
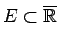 apakšējo robežu
un apakšējo slieksni, augšējo robežu un augšējo slieksni.
Tikai šoreiz tie var būt arī
bezgalīgi.
apakšējo robežu
un apakšējo slieksni, augšējo robežu un augšējo slieksni.
Tikai šoreiz tie var būt arī
bezgalīgi.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
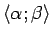 1.17
1.17
- Šoreiz
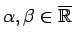 ;
;
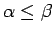 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... eksistē1.18
- [fr. exister; lat. exsistere rasties, izcelties] -
pastāvēt, būt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Funkcija2.1
- [lat. functio izpilde, darbība] - atkarīgais
mainīgais lielums.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Lobačevskis2.2
- Nikolajs
Lobačevskis - krievu mat. (1792 - 1856).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Dirihlē2.3
- Ležens Dirihlē - franču mat. (1805 - 1859).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... atbilstību2.4
- Visbiežāk apzīmēsim ar
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
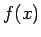 2.5
2.5
- Tā bieži apzīmē
arī pašu funkciju un saka: ``funkcija
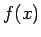 ''. Šoreiz ar
''. Šoreiz ar  saprot
patvaļīgo kopas
saprot
patvaļīgo kopas 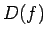 elementu.
elementu.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... funkciju2.6
- Šoreiz
 un
un 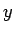 ir reālie skaitļi.
ir reālie skaitļi.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... formulu2.7
- [lat. formula forma, noteikta kārtula] -
lielumu kopums, kuri izteikti ar skaitļiem un burtiem un
savienoti ar matemātiskām zīmēm.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... grafiku2.8
- [gr. graphikos
uz rakstīšanu, zīmēšanu
attiecīgs].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... daļa2.9
- Lielākais
veselais skaitlis, kas nepārsniedz
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... daļa2.10
-
![$ \{x\}=x-[x]$](img211.gif) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
funkcijām2.11
- Šoreiz ir domātas skaitliskas funkcijas, t.i.,
tādas funkcijas, kurām vērtības ir skaitļi.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... funkciju2.12
- Šādu operāciju var izdarīt
arī vairākas reizes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... funkciju2.13
- Skaitliskas
funkcijas gadījumā virkni nosauksim par skaitļu
virkni.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... progresija2.14
- [lat. progressio kustība uz
priekšu; attīstība].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 2.15
2.15
- Šeit un turpmāk sapratīsim reālā mainīgā reālu
funkciju.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...monotonām2.16
- [gr. monos viens, viens
vienīgs, vienīgais
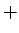 ton(i)s vienmuļīgs, garlaicīgs] - tāds, kas
mainās vienā virzienā.
ton(i)s vienmuļīgs, garlaicīgs] - tāds, kas
mainās vienā virzienā.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... funkciju2.17
- [gr. periodos apkārtceļš, riņķojums].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... periodu2.18
- Turpmāk ar
šādu skaitli sapratīsim
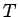 un nosauksim vienkārši par periodu.
un nosauksim vienkārši par periodu.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...funkciju2.19
- Bieži funkcijas
 apvērsto funkciju apzīmē
apvērsto funkciju apzīmē
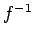 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... augšas2.20
- Eksistē tāds
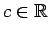 , ka visiem
, ka visiem 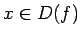 izpildās nevienādība
izpildās nevienādība
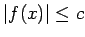 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...konverģē3.1
- [fr. converger saiet vienā punktā; lat.
convergere tiekties].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (skat.3.2
- Simbols
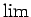 ir latīņu valodas vārda limes (robeža) jeb tādas pašas
nozīmes franču valodas vārda limits saīsinājums.
ir latīņu valodas vārda limes (robeža) jeb tādas pašas
nozīmes franču valodas vārda limits saīsinājums.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...diverģentām3.3
- [lat. divergens (divergentis) dažādos virzienos
ejošs].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Bernulli3.4
- Jēkabs
Bernulli - šveiciešu matemātiķis (1654-1705).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (skat.3.5
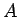 var būt gan skaitlis,
gan viens no simboliem
var būt gan skaitlis,
gan viens no simboliem 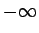 ,
, 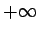 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... zīmes3.6
- Simbolu
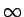 (bezgalība bez zīmes)
atšķirībā no iepriekš apskatītajiem simboliem
(bezgalība bez zīmes)
atšķirībā no iepriekš apskatītajiem simboliem 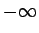 un
un 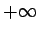 saista ar reāliem skaitļiem tikai tā apkārtnes. Ar simbola
saista ar reāliem skaitļiem tikai tā apkārtnes. Ar simbola 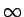
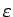 - apkārtni sapratīsim šādu kopu
- apkārtni sapratīsim šādu kopu
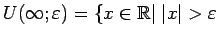 , t.i.,
simbolu
, t.i.,
simbolu 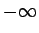 un
un 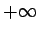
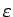 - apkārtņu apvienojumu.
- apkārtņu apvienojumu.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
radiāni3.7
- [lat. radius stars, rādiuss] - leņķa mērvienība,
apmēram
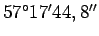 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... patstāvīgi3.8
- Izmantojot pretējā pieņēmuma
paņēmienu un 3.16. teorēmu.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
(skat.3.9
- [lat. signum - zīme].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... funkciju3.10
- Parasti šādas funkcijas apzīmē ar
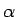 ,
, 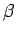 ,
, 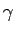 utt.
utt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (skat.3.11
- Lasa:
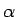 vienāds ar omikrons (grieķu alfabēta burts) no
vienāds ar omikrons (grieķu alfabēta burts) no
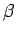
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...ekvivalentām3.12
- [lat. aequivalens]
kaut kas līdzvērtīgs, ar tādu pašu nozīmi, tik pat stiprs.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... diskrēti3.13
- Šoreiz
![$ [x]$](img756.gif) vērtības ir naturāli skaitļi.
vērtības ir naturāli skaitļi.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Bolcano
3.14
- Bernhards Bolcano - čehu filozofs un matemātiķis (1781-1848).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Veierštrāsa3.15
- Kārlis Veierštrāss - vācu matemātiķis (1815-1897).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Košī3.16
- Ogistens Košī -
franču matemātiķis (1789-1857)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
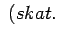 3.17
3.17
- Šādu virkni
sauksim par fundamentālu virkni.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Heines4.1
- Heinrihs Heine - vācu matemātiķis (1821 - 1881)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... punktā4.2
- Šoreiz funkcija ir definēta punkta
 apkārtnē.
apkārtnē.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... slieksnis4.3
- Ar
funkcijas
 augšējo slieksni kopā
augšējo slieksni kopā 
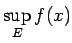 sapratīsim šīs funkcijas atbilstošas vērtību kopas
sapratīsim šīs funkcijas atbilstošas vērtību kopas 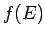 augšējo
slieksni, t.i.,
augšējo
slieksni, t.i.,
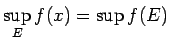 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Kantora4.4
- Georgs Kantors - vācu matemātiķis,
mūsdienu kopu teorijas pamatlicējs (1845 - 1918)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.