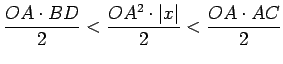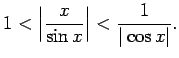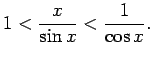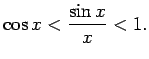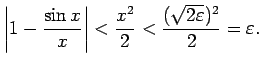Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.5. Teorēmas par funkcijas galīgajām robežām
Augstāk: 3. ROBEŽA
Iepriekšējais: 3.3. Funkcijas robežas vienīgums
-
3.4. teorēma.
- Sinusa attiecības pret argumentu robeža, kad
arguments tiecas uz nulli, ir vienāda ar
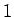 , t.i.,
, t.i.,
 Apskatīsim vienības riņķa līniju un
izveidosim divus taisnleņķa trijstūrus
Apskatīsim vienības riņķa līniju un
izveidosim divus taisnleņķa trijstūrus 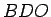 un
un 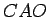 (3.22. zīm.) ar kopējo šauro leņķi
(3.22. zīm.) ar kopējo šauro leņķi  radiāni3.7
radiāni3.7
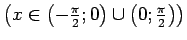 .
.
Loka 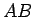 garums būs
garums būs 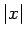 ,
,
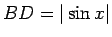 ,
,
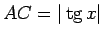 .
Salīdzinot trijstūra
.
Salīdzinot trijstūra 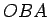 , sektora
, sektora 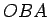 un trijstūra
un trijstūra 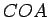 laukumus, iegūsim nevienādību
laukumus, iegūsim nevienādību
jeb
Izdalīsim šo nevienādību ar
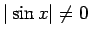 . Iegūsim nevienādību
Minētajām argumenta
. Iegūsim nevienādību
Minētajām argumenta  vērtībām
vērtībām
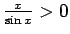 un
un 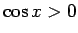 , tāpēc
Tādējādi
No šīs nevienādības izriet, ka
(Izmantojām, ka
, tāpēc
Tādējādi
No šīs nevienādības izriet, ka
(Izmantojām, ka
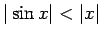 , tādējādi
, tādējādi
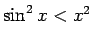 ). Esam
ieguvuši, ka
Izvēlēsimies
). Esam
ieguvuši, ka
Izvēlēsimies
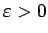 un
un
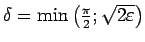 .
.
Visiem
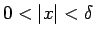 izpildīsies
Saskaņā ar funkcijas robežas definīciju
izpildīsies
Saskaņā ar funkcijas robežas definīciju
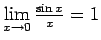 . (Acīmredzami, funkcija
. (Acīmredzami, funkcija
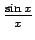 ir definēta punkta
ir definēta punkta 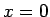 pārdurtā apkārtnē.)
pārdurtā apkārtnē.)



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.5. Teorēmas par funkcijas galīgajām robežām
Augstāk: 3. ROBEŽA
Iepriekšējais: 3.3. Funkcijas robežas vienīgums
2003-02-24
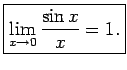
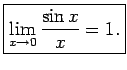
![]() Apskatīsim vienības riņķa līniju un
izveidosim divus taisnleņķa trijstūrus
Apskatīsim vienības riņķa līniju un
izveidosim divus taisnleņķa trijstūrus ![]() un
un ![]() (3.22. zīm.) ar kopējo šauro leņķi
(3.22. zīm.) ar kopējo šauro leņķi ![]() radiāni3.7
radiāni3.7
![]() .
.
![]() garums būs
garums būs ![]() ,
,
![]() ,
,
![]() .
Salīdzinot trijstūra
.
Salīdzinot trijstūra ![]() , sektora
, sektora ![]() un trijstūra
un trijstūra ![]() laukumus, iegūsim nevienādību
laukumus, iegūsim nevienādību