![]() Pieņemsim pretējo, t.i., ka
Pieņemsim pretējo, t.i., ka
![]() un
un
![]() , kur
, kur
![]() (izņemot
gadījumu, kad viena no tām ir bezgalība, bet otra - bezgalība ar
zīmi). Izvēlēsimies punktu
(izņemot
gadījumu, kad viena no tām ir bezgalība, bet otra - bezgalība ar
zīmi). Izvēlēsimies punktu ![]() un
un ![]() apkārtnes
apkārtnes ![]() un
un
![]() , kas nešķeļas, t.i., tādas, lai
, kas nešķeļas, t.i., tādas, lai
![]() . Saskaņā ar funkcijas robežas definīciju punkta
. Saskaņā ar funkcijas robežas definīciju punkta
![]() jebkurai apkārtnei
jebkurai apkārtnei ![]() eksistē punkta
eksistē punkta ![]() tāda apkārtne
tāda apkārtne
![]() , ka visiem
, ka visiem
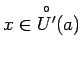 ,
izpildīsies sakarība
,
izpildīsies sakarība
![]() . Analoģiski punkta
. Analoģiski punkta ![]() jebkurai apkārtnei
jebkurai apkārtnei ![]() eksistē punkta
eksistē punkta ![]() tāda apkārtne
tāda apkārtne
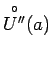 , ka visiem
, ka visiem
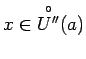 , izpildīsies sakarība
, izpildīsies sakarība
![]() . Izvēlēsimies
. Izvēlēsimies
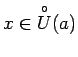 , kur
, kur
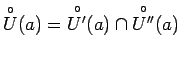 .
Šādiem
.
Šādiem ![]() vienlaicīgi izpildīsies sakarības
vienlaicīgi izpildīsies sakarības
![]() un
un
![]() , kas ir pretrunā ar pieņēmumu, ka šīs apkārtnes
nešķeļas (3.21. zīm.).
, kas ir pretrunā ar pieņēmumu, ka šīs apkārtnes
nešķeļas (3.21. zīm.).
Pieņēmums, ka funkcijai ![]() var būt divas dažādas robežas, nav
pareizs.
var būt divas dažādas robežas, nav
pareizs.
![]()