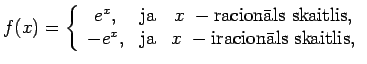Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.3. Funkcijas robežas vienīgums
Augstāk: 3. ROBEŽA
Iepriekšējais: 3.1.3. Skaitļu virkņu bezgalīgas robežas
Apskatīsim funkciju  , definētu punkta
, definētu punkta  apkārtnē, izņemot
varbūt šo punktu.
apkārtnē, izņemot
varbūt šo punktu.
-
3.5. definīcija.
- Par punkta
 pārdurtu apkārtni nosauksim šī
punkta apkārtni bez punkta
pārdurtu apkārtni nosauksim šī
punkta apkārtni bez punkta  un apzīmēsim ar
un apzīmēsim ar
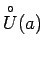 .
.
-
3.6. definīcija.
- (Funkcijas robežas vispārīgā definīcija).
Punktu 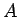 nosauksim par funkcijas
nosauksim par funkcijas  robežu punktā
robežu punktā  , ja
punkta
, ja
punkta 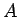 jebkurai apkārtnei
jebkurai apkārtnei 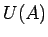 eksistē punkta
eksistē punkta  tāda
pārdurta apkārtne
tāda
pārdurta apkārtne
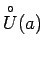 , ka visiem
, ka visiem
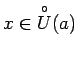 izpildās sakarība
izpildās sakarība
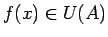 (3.3. zīm.). Pierakstīsim
(3.3. zīm.). Pierakstīsim
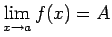
vai
![$\displaystyle \quad f(x)\xrightarrow[x\rightarrow a]{\;}A\/.$](img437.gif)
Nosacījums, ka 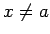 , ir būtisks. Pretējā gadījumā funkcijai
, ir būtisks. Pretējā gadījumā funkcijai
punktā 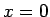 neeksistētu robeža. Tagad
neeksistētu robeža. Tagad
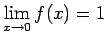 . (3.4. zīm.)
. (3.4. zīm.)
Apskatīsim funkcijas robežas vispārīgās definīcijas atsevišķus
gadījumus.
-
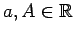 .
.
Šoreiz par punkta apkārtni būs vaļējs intervāls ar centru šajā
punktā un atbilstošu rādiusu. Apkārtnes varēs uzdot ar
apkārtņu rādiusu
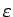 un
un 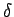 palīdzību.
palīdzību.
Skaitli 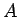 nosauksim par funkcijas
nosauksim par funkcijas  robežu punktā
robežu punktā  (
( -
skaitlis), ja jebkuram
-
skaitlis), ja jebkuram
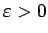 eksistē tāds
eksistē tāds 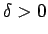 (atkarīgs no
(atkarīgs no
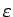 ), ka visiem
), ka visiem
 , kuriem
, kuriem
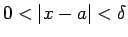 , izpildās nevienādība
No ģeometriskā viedokļa tas nozīmē,
lai cik šaura arī nebūtu horizontālā josla starp taisnēm
, izpildās nevienādība
No ģeometriskā viedokļa tas nozīmē,
lai cik šaura arī nebūtu horizontālā josla starp taisnēm
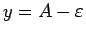 un
un
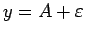 , funkcijas grafiks
(izņemot varbūt punktu
, funkcijas grafiks
(izņemot varbūt punktu
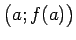 ) visiem
) visiem
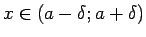 atrodas šajā joslā (3.5. zīm.).
atrodas šajā joslā (3.5. zīm.).
-
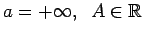 .
.
Šoreiz punkta 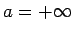 apkārtni varēs uzdot ar apkārtnes
rādiusa
apkārtni varēs uzdot ar apkārtnes
rādiusa
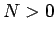 palīdzību. Par punkta
palīdzību. Par punkta 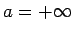
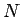 -apkārtni būs vaļējs intervāls
-apkārtni būs vaļējs intervāls
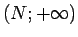 .
.
Skaitli 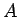 nosauksim par funkcijas
nosauksim par funkcijas  robežu punktā
robežu punktā
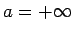 , ja jebkuram
, ja jebkuram
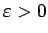 eksistē tāds
eksistē tāds 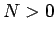 , ka visiem
, ka visiem  , kuriem
, kuriem 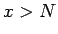 , izpildās
nevienādība
No ģeometriskā viedokļa tas nozīmē, lai cik šaura arī nebūtu
horizontālā josla starp taisnēm
, izpildās
nevienādība
No ģeometriskā viedokļa tas nozīmē, lai cik šaura arī nebūtu
horizontālā josla starp taisnēm
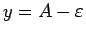 un
un
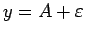 , funkcijas grafiks visiem
, funkcijas grafiks visiem 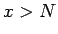 atrodas šajā
joslā (3.6. zīm.).
atrodas šajā
joslā (3.6. zīm.).
-
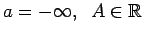 .
.
Skaitli 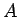 nosauksim par funkcijas
nosauksim par funkcijas  robežu punktā
robežu punktā
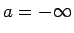 , ja jebkuram
, ja jebkuram
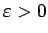 eksistē tāds
eksistē tāds 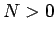 , ka visiem
, ka visiem  , kuriem
, kuriem 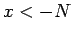 , izpildās
nevienādība
, izpildās
nevienādība
-
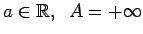 (3.8. zīm.).
(3.8. zīm.).
-
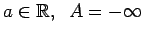 (3.9. zīm.).
(3.9. zīm.).
-
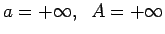 (3.10. zīm.).
(3.10. zīm.).
-
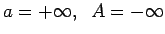 (3.11. zīm.).
(3.11. zīm.).
-
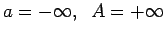 (3.12. zīm.).
(3.12. zīm.).
-
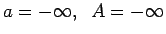 .
.
Simbolu 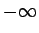 nosauksim par funkcijas
nosauksim par funkcijas  robežu punktā
robežu punktā
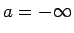 , ja jebkuram
, ja jebkuram 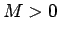 eksistē tāds
eksistē tāds 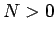 , ka visiem
, ka visiem
 , kuriem
, kuriem 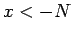 , izpildās nevienādība
, izpildās nevienādība 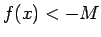 .
.
No ģeometriskā viedokļa tas nozīmē: lai cik liels arī nebūtu
skaitlis 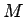 visiem
visiem 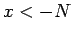 funkcijas grafiks
funkcijas grafiks  rodas zem
taisnes
rodas zem
taisnes 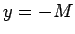 (3.13. zīm.).
(3.13. zīm.).
-
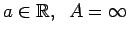 (bez zīmes3.6)
(3.14. zīm.).
(bez zīmes3.6)
(3.14. zīm.).
-
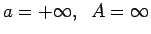 .
.
Simbolu 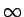 nosauksim par funkcijas
nosauksim par funkcijas  robežu punktā
robežu punktā
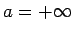 , ja jebkuram
, ja jebkuram 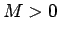 eksistē tāds
eksistē tāds 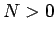 , ka visiem
, ka visiem
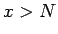 izpildās nevienādība
izpildās nevienādība 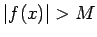 , t.i.,
, t.i., 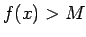 vai
vai
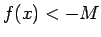 .
.
Piemēram, funkcijai
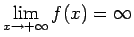 .
.
No ģeometriskā viedokļa tas nozīmē, lai cik liels arī nebūtu
skaitlis 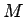 , visiem
, visiem 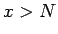 funkcijas grafiks atrodas virs
taisnes
funkcijas grafiks atrodas virs
taisnes 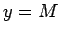 vai zem taisnes
vai zem taisnes 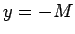 (3.15. zīm.).
(3.15. zīm.).
-
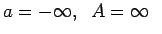 3.16. zīm.
3.16. zīm.
-
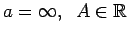 .
.
Skaitli 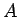 nosauksim par funkcijas
nosauksim par funkcijas  robežu punktā
robežu punktā
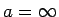 , ja jebkuram
, ja jebkuram
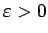 eksistē tāds
eksistē tāds 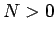 , ka visiem
, ka visiem  , kuriem
, kuriem 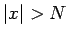 , izpildās
nevienādība
, izpildās
nevienādība
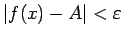 .
.
No ģeometriskā viedokļa tas nozīmē, lai cik šaura arī nebūtu
horizontālā josla starp taisnēm
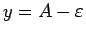 ,
,
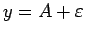 , funkcijas grafiks visiem
, funkcijas grafiks visiem 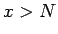 vai
vai 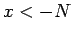 atradīsies šajā joslā (3.17. zīm.).
atradīsies šajā joslā (3.17. zīm.).
-
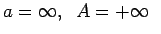 (3.18. zīm.).
(3.18. zīm.).
-
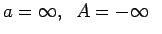 (3.19. zīm.).
(3.19. zīm.).
-
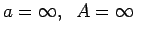 (3.20. zīm.).
(3.20. zīm.).



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.3. Funkcijas robežas vienīgums
Augstāk: 3. ROBEŽA
Iepriekšējais: 3.1.3. Skaitļu virkņu bezgalīgas robežas
2003-02-24
![]() , definētu punkta
, definētu punkta ![]() apkārtnē, izņemot
varbūt šo punktu.
apkārtnē, izņemot
varbūt šo punktu.
![]() nosauksim par funkcijas
nosauksim par funkcijas ![]() robežu punktā
robežu punktā ![]() , ja
punkta
, ja
punkta ![]() jebkurai apkārtnei
jebkurai apkārtnei ![]() eksistē punkta
eksistē punkta ![]() tāda
pārdurta apkārtne
tāda
pārdurta apkārtne
![]() , ka visiem
, ka visiem
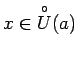 izpildās sakarība
izpildās sakarība
![]() (3.3. zīm.). Pierakstīsim
(3.3. zīm.). Pierakstīsim
![]() , ir būtisks. Pretējā gadījumā funkcijai
, ir būtisks. Pretējā gadījumā funkcijai