


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.2. Reālā mainīgā reālās funkcijas robeža
Augstāk: 3.1. Skaitļu virknes robeža
Iepriekšējais: 3.1.2. Bernulli nevienādība
-
3.2. definīcija.
- Simbolu
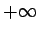 nosauksim par virknes
nosauksim par virknes 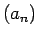 robežu, ja jebkuram pozitīvam skaitlim
robežu, ja jebkuram pozitīvam skaitlim 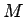 eksistē tāds
naturāls skaitlis
eksistē tāds
naturāls skaitlis 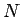 , ka visiem
, ka visiem 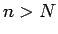 izpildās nevienādība
izpildās nevienādība
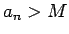 . Pierakstīsim
. Pierakstīsim
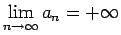 un teiksim, ka
virkne diverģē, pie tam uz
un teiksim, ka
virkne diverģē, pie tam uz 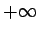 .
.
Nevienādība 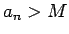 nozīmē, ka visiem
nozīmē, ka visiem 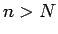
Šīs apkārtnes ārpusē atradīsies galīgs skaits virknes locekļu.
Acīmredzami, šāda virkne nav ierobežota no augšas. Apgrieztais
apgalvojums nav spēkā.
-
3.3. definīcija.
- Simbolu
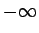 nosauksim par virknes
nosauksim par virknes 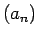 robežu, ja jebkuram pozitīvam skaitlim
robežu, ja jebkuram pozitīvam skaitlim 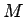 eksistē tāds
naturāls skaitlis
eksistē tāds
naturāls skaitlis 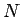 , ka visiem
, ka visiem 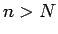 izpildās nevienādība
izpildās nevienādība
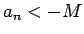 . Pierakstīsim
. Pierakstīsim
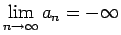 un teiksim, ka
virkne diverģē, pie tam uz
un teiksim, ka
virkne diverģē, pie tam uz 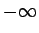 .
.
Nevienādība 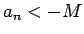 nozīmē, ka visiem
nozīmē, ka visiem 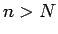
Šī virkne nav ierobežota no apakšas.
Iepriekš apskatītās virkņu robežu definīcijas var apvienot vienā -
virknes robežas vispārīgajā definīcijā. Tam nolūkam izmantosim
apkārtnes jēdzienu.
-
3.4. definīcija.
- (Virknes robežas vispārīgā definīcija).
Punktu 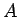 (skat.3.5) nosauksim par
virknes
(skat.3.5) nosauksim par
virknes 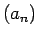 robežu, ja šī punkta jebkurai apkārtnei
robežu, ja šī punkta jebkurai apkārtnei 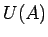 eksistē tāds naturāls skaitlis
eksistē tāds naturāls skaitlis 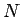 , ka visiem
, ka visiem 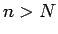 izpildās
sakarība
izpildās
sakarība
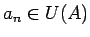 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.2. Reālā mainīgā reālās funkcijas robeža
Augstāk: 3.1. Skaitļu virknes robeža
Iepriekšējais: 3.1.2. Bernulli nevienādība
2003-02-24
![]() nozīmē, ka visiem
nozīmē, ka visiem ![]()
![]() nozīmē, ka visiem
nozīmē, ka visiem ![]()
![]() (skat.3.5) nosauksim par
virknes
(skat.3.5) nosauksim par
virknes ![]() robežu, ja šī punkta jebkurai apkārtnei
robežu, ja šī punkta jebkurai apkārtnei ![]() eksistē tāds naturāls skaitlis
eksistē tāds naturāls skaitlis ![]() , ka visiem
, ka visiem ![]() izpildās
sakarība
izpildās
sakarība
![]() .
.