


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.1.3. Skaitļu virkņu bezgalīgas robežas
Augstāk: 3.1. Skaitļu virknes robeža
Iepriekšējais: 3.1.1. Konverģenta skaitļu virkne
-
3.2. teorēma.
- Visiem naturāliem skaitļiem
 un visiem
un visiem 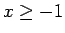 izpildās Bernulli3.4 nevienādība
izpildās Bernulli3.4 nevienādība
 Pierādīsim šo nevienādību, izmantojot
matemātiskās indukcijas metodi.
Pierādīsim šo nevienādību, izmantojot
matemātiskās indukcijas metodi.
Acīmredzami, pie 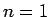 sakarība izpildās, pie tam iegūsim
vienādību
sakarība izpildās, pie tam iegūsim
vienādību 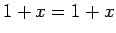 .
.
Pieņemsim, ka minētā sakarība ir spēkā pie 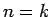 , t.i., visiem
, t.i., visiem
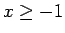 izpildās nevienādība
Pareizināsim šīs nevienādības abas puses ar
izpildās nevienādība
Pareizināsim šīs nevienādības abas puses ar 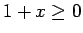 :
:
Iegūtā nevienādība
nozīmē, ka teorēmā minētā sakarība ir spēkā pie 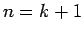 . Saskaņā
ar matemātiskās indukcijas metodi Bernulli nevienādība ir
pierādīta.
. Saskaņā
ar matemātiskās indukcijas metodi Bernulli nevienādība ir
pierādīta.
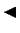
Acīmredzami, tikai tajos gadījumos, kad 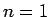 vai
vai 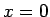 , iegūsim
vienādību.
, iegūsim
vienādību.
Izmantojot Bernulli nevienādību, pierādīsim, ka
![$ \lim\limits_{n\rightarrow\infty}\sqrt[n]{a}=1$](img408.gif)
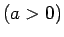 .
.
- Izvēlēsimies
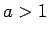 un naturālu skaitli
un naturālu skaitli
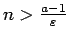 , kur
, kur
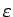 ir jebkurš
pozitīvs skaitlis. No Bernulli nevienādības un
nevienādības
ir jebkurš
pozitīvs skaitlis. No Bernulli nevienādības un
nevienādības
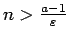 iegūsim, ka
No kurienes
Tātad
Tas nozīmē, ka
iegūsim, ka
No kurienes
Tātad
Tas nozīmē, ka
- Izvēlēsimies
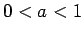 un apzīmēsim
un apzīmēsim
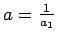 , kur
, kur
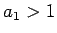 . Tad
(jo
. Tad
(jo
![$ \sqrt[n]{a_1}>1$](img420.gif) ). Saskaņā ar 1. gadījumu pietiekoši
lieliem
). Saskaņā ar 1. gadījumu pietiekoši
lieliem  izpildīsies nevienādība
Tāpēc arī
Tas nozīmē, ka
izpildīsies nevienādība
Tāpēc arī
Tas nozīmē, ka
- Izvēlēsimies
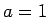 . Šoreiz
. Šoreiz
![$ \sqrt[n]{a}=1$](img422.gif) un
Tas nozīmē, ka
un
Tas nozīmē, ka



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.1.3. Skaitļu virkņu bezgalīgas robežas
Augstāk: 3.1. Skaitļu virknes robeža
Iepriekšējais: 3.1.1. Konverģenta skaitļu virkne
2003-02-24
![]() Pierādīsim šo nevienādību, izmantojot
matemātiskās indukcijas metodi.
Pierādīsim šo nevienādību, izmantojot
matemātiskās indukcijas metodi.
![$\displaystyle \left\vert\sqrt[n]{a}-1\right\vert=\left\vert\frac{1}{\sqrt[n]{a_...
...\sqrt[n]{a_1}-1}{\sqrt[n]{a_1}}\right\vert<\left\vert\sqrt[n]{a_1}-1\right\vert$](img419.gif)