


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.1.2. Bernulli nevienādība
Augstāk: 3.1. Skaitļu virknes robeža
Iepriekšējais: 3.1. Skaitļu virknes robeža
-
3.1. definīcija.
- Skaitli
 nosauksim par virknes
nosauksim par virknes 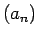 robežu,
ja jebkuram
robežu,
ja jebkuram
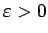 eksistē tāds
naturāls skaitlis
eksistē tāds
naturāls skaitlis 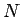 (atkarīgs no
(atkarīgs no
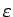 ), ka visiem
), ka visiem
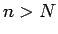 izpildās nevienādība
izpildās nevienādība
Tādos gadījumos teiksim, ka virkne 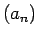 konverģē3.1 uz
konverģē3.1 uz  un rakstīsim
un rakstīsim
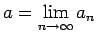 (skat.3.2) vai
(skat.3.2) vai
![$ a_n\xrightarrow[n\rightarrow\infty]{\;}a$](img360.gif) . Nevienādība
. Nevienādība
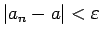 ir līdzvērtīga nevienādībām
ir līdzvērtīga nevienādībām
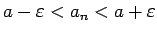 . Tas nozīmē, ka visiem
. Tas nozīmē, ka visiem 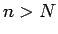
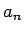 pieder punkta
pieder punkta 
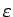 - apkārtnei, t.i.,
- apkārtnei, t.i.,
Ārpus šīs apkārtnes atrodas tikai galīgs skaits virknes locekļu
(3.1. zīm.). Šis numurs 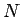 ir atkarīgs no apkārtnes
rādiusa
ir atkarīgs no apkārtnes
rādiusa
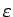 .
.
Apskatīsim dažus piemērus.
-
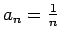 . Virkne konverģē un tās robeža
. Virkne konverģē un tās robeža 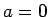 ,
jo visiem
,
jo visiem
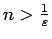 izpildīsies nevienādība
Tāpēc par
izpildīsies nevienādība
Tāpēc par 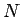 var paņemt skaitļa
var paņemt skaitļa
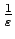 veselo daļu
veselo daļu
![$ \left[\frac{1}{\varepsilon}\right]$](img370.gif) . Tagad visiem
. Tagad visiem
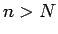 , kur
, kur
![$ N=\left[\frac{1}{\varepsilon}\right]$](img371.gif) , izpildīsies
nevienādība
, izpildīsies
nevienādība
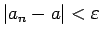 . Tātad
. Tātad
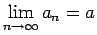 , t.i.,
, t.i.,
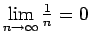 . Ja
izvēlēsimies, piemēram,
. Ja
izvēlēsimies, piemēram,
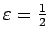 , tad
, tad 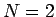 un, sākot ar
un, sākot ar 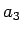 , visi šīs virknes locekļi atradīsies
intervāla
, visi šīs virknes locekļi atradīsies
intervāla
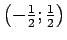 iekšienē
(3.2. zīm.).
iekšienē
(3.2. zīm.).
-
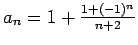 . Virkne konverģē un tās
robeža
. Virkne konverģē un tās
robeža 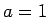 , jo paņemot
, jo paņemot
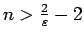 ,
izpildīsies nevienādība
Tāpēc visiem
izpildīsies nevienādība
,
izpildīsies nevienādība
Tāpēc visiem
izpildīsies nevienādība
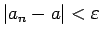 . Tātad
. Tātad
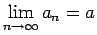 , t.i.,
, t.i.,
-
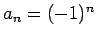 . Ja pieņemtu, ka virkne konverģē un
skaitlis
. Ja pieņemtu, ka virkne konverģē un
skaitlis  ir tās robeža, tad, piemēram, skaitlim
ir tās robeža, tad, piemēram, skaitlim
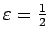 varēs sameklēt tādu
varēs sameklēt tādu 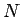 , ka visiem
, ka visiem
 un
un 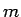 lielākiem par
lielākiem par 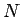 vienlaicīgi izpildīsies
nevienādības
Tad
Ieguvām pretunu, jo starpība
vienlaicīgi izpildīsies
nevienādības
Tad
Ieguvām pretunu, jo starpība 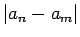 ir 0
vai
ir 0
vai 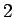 , bet mēs esam ieguvuši, ka
, bet mēs esam ieguvuši, ka
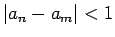 . Tātad
. Tātad
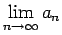 neeksistē, un tāpēc virkne nav
konverģenta. Turpmāk šādas virknes nosauksim par
diverģentām3.3 virknēm.
neeksistē, un tāpēc virkne nav
konverģenta. Turpmāk šādas virknes nosauksim par
diverģentām3.3 virknēm.
-
3.1. teorēma.
- Konverģenta virkne ir ierobežota.
 Apskatīsim konverģentu virkni
Apskatīsim konverģentu virkni 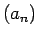 . Tad
eksistē skaitlis
. Tad
eksistē skaitlis  , kur
, kur
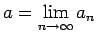 .
Saskaņā ar virknes robežas definīciju jebkuram
.
Saskaņā ar virknes robežas definīciju jebkuram
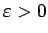 ,
piemēram,
,
piemēram,
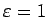 eksistē tāds naturāls skaitlis
eksistē tāds naturāls skaitlis 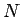 , ka
visiem
, ka
visiem 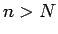 izpildīsies nevienādība
izpildīsies nevienādība
t.i.,
Virkne ir ierobežota, jo visiem 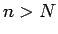 izpildās nevienādība
izpildās nevienādība
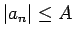 , kur
, kur
Acīmredzami, ka šai teorēmai apgrieztā teorēma nav spēkā.
Piemēram,
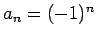 ir ierobežota, bet nav konverģenta (tātad
ir diverģenta) virkne.
ir ierobežota, bet nav konverģenta (tātad
ir diverģenta) virkne.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.1.2. Bernulli nevienādība
Augstāk: 3.1. Skaitļu virknes robeža
Iepriekšējais: 3.1. Skaitļu virknes robeža
2003-02-24
![]() konverģē3.1 uz
konverģē3.1 uz ![]() un rakstīsim
un rakstīsim
![]() (skat.3.2) vai
(skat.3.2) vai
![]() . Nevienādība
. Nevienādība
![]() ir līdzvērtīga nevienādībām
ir līdzvērtīga nevienādībām
![]() . Tas nozīmē, ka visiem
. Tas nozīmē, ka visiem ![]()
![]() pieder punkta
pieder punkta ![]()
![]() - apkārtnei, t.i.,
- apkārtnei, t.i.,
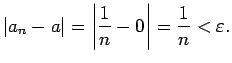
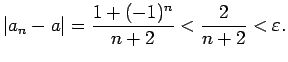
![$\displaystyle n>N=\max\left(\left[\frac{2}{\varepsilon}-2\right];1\right)$](img383.gif)
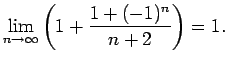
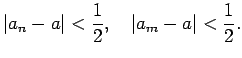
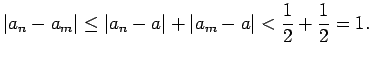
![]() Apskatīsim konverģentu virkni
Apskatīsim konverģentu virkni ![]() . Tad
eksistē skaitlis
. Tad
eksistē skaitlis ![]() , kur
, kur
![]() .
Saskaņā ar virknes robežas definīciju jebkuram
.
Saskaņā ar virknes robežas definīciju jebkuram
![]() ,
piemēram,
,
piemēram,
![]() eksistē tāds naturāls skaitlis
eksistē tāds naturāls skaitlis ![]() , ka
visiem
, ka
visiem ![]() izpildīsies nevienādība
izpildīsies nevienādība
![]() ir ierobežota, bet nav konverģenta (tātad
ir diverģenta) virkne.
ir ierobežota, bet nav konverģenta (tātad
ir diverģenta) virkne.