Turpmāk vienosimies apskatīt tikai tādas funkcijas, kas definētas punkta
Turpmāk vienosimies apskatīt tikai tādas funkcijas, kas definētas
punkta ![]() apkārtnē, izņemot varbūt pašu šo punktu. Ar punkta
apkārtnē, izņemot varbūt pašu šo punktu. Ar punkta
![]() apkārtni sapratīsim šī punkta pārdurto apkārtni.
apkārtni sapratīsim šī punkta pārdurto apkārtni.
![]() Saskaņā ar galīgas robežas definīciju
jebkuram
Saskaņā ar galīgas robežas definīciju
jebkuram
![]() , tai skaitā
, tai skaitā
![]() , eksistē
punkta
, eksistē
punkta ![]() tāda apkārtne
tāda apkārtne
![]() , ka visiem
, ka visiem
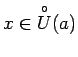 , izpildīsies nevienādība
, izpildīsies nevienādība
Teorēmai apgrieztais apgalvojums nav spēkā, piemēram, Dirihlē funkcija

![]() Jebkuram
Jebkuram
![]() un katram
un katram ![]() no
minētās apkārtnes izpildīsies nevienādība
no
minētās apkārtnes izpildīsies nevienādība
![]() . Tātad
. Tātad
![]() .
.
![]()
![]() Saskaņā ar funkcijas
Saskaņā ar funkcijas ![]() robežas
robežas ![]() definīciju jebkuram
definīciju jebkuram
![]() eksistē punkta
eksistē punkta ![]() tāda
apkārtne
tāda
apkārtne
![]() , ka visiem
, ka visiem
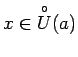 izpildīsies nevienādība
izpildīsies nevienādība
(Pierādīt patstāvīgi)
![]() Saskaņā ar funkcijas
Saskaņā ar funkcijas ![]() robežas
robežas ![]() definīciju jebkuram
definīciju jebkuram
![]() eksistē tāda punkta
eksistē tāda punkta ![]() apkārtne
apkārtne
![]() , ka visiem
, ka visiem
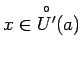 izpildīsies nevienādība
izpildīsies nevienādība
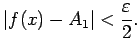
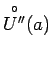 , ka visiem
, ka visiem
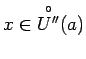 izpildīsies nevienādība
izpildīsies nevienādība
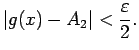
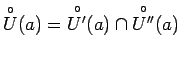 .
Tagad visiem
.
Tagad visiem
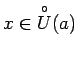 šīs divas nevienādības
izpildīsies vienlaicīgi.
šīs divas nevienādības
izpildīsies vienlaicīgi.
Tāpēc
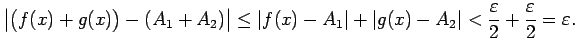
Ar matemātiskās indukcijas metodi šo teorēmu var vispārināt uz jebkura galīga skaita funkciju summu.
3.9. teorēmai apgrieztais apgalvojums nav pareizs, piemēram, funkcijām
![]() Gadījumā, kad
Gadījumā, kad ![]() , funkcija
, funkcija
![]() const. Robeža eksistē un, acīmredzami, izpildās
teorēmā minētā vienādība.
const. Robeža eksistē un, acīmredzami, izpildās
teorēmā minētā vienādība.
Apskatīsim gadījumu, kad
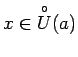 izpildīsies nevienādība
izpildīsies nevienādība
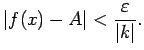
Ja ![]() , iegūsim:
, iegūsim:
Izmantojot vēl 3.9. teorēmu, iegūsim:
![]() Tā kā funkcija
Tā kā funkcija ![]() ierobežota punkta
ierobežota punkta ![]() apkārtnē
apkārtnē ![]() , tad visiem
, tad visiem
![]() , izpildīsies nevienādība
, izpildīsies nevienādība
![]() . Saskaņā ar funkcijas
. Saskaņā ar funkcijas ![]() robežas definīciju
jebkuram
robežas definīciju
jebkuram
![]() eksistē punkta
eksistē punkta ![]() tāda apkārtne
tāda apkārtne
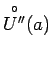 , ka visiem
, ka visiem
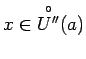 izpildīsies nevienādība
izpildīsies nevienādība
![]() . Apzīmēsim
ar
. Apzīmēsim
ar
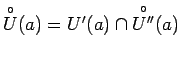 . Tagad
visiem
. Tagad
visiem
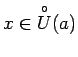 abas nevienādības izpildīsies
vienlaicīgi, tāpēc
abas nevienādības izpildīsies
vienlaicīgi, tāpēc
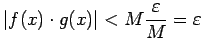
![]() Funkciju
Funkciju ![]() un
un ![]() reizinājumu uzrakstīsim
šādi:
reizinājumu uzrakstīsim
šādi:
Ar matemātiskās indukcijas metodi šo teorēmu var vispārināt uz jebkura galīga skaita funkciju reizinājumu, tai skaitā
3.12. teorēmai apgrieztais apgalvojums nav spēkā.
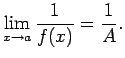
![]() Saskaņā ar 3.7. teorēmu
Saskaņā ar 3.7. teorēmu
![]() . Izvēlēsimies punkta
. Izvēlēsimies punkta
![]() tādu apkārtni, kas nesatur punktu 0, t.i.,
tādu apkārtni, kas nesatur punktu 0, t.i.,
![]() , kur, piemēram,
, kur, piemēram,
![]() . Saskaņā ar funkcijas
. Saskaņā ar funkcijas ![]() robežas
robežas
![]() definīciju izvēlētajai punkta
definīciju izvēlētajai punkta ![]() apkārtnei eksistē punkta
apkārtnei eksistē punkta
![]() tāda apkārtne
tāda apkārtne
![]() , ka visiem
, ka visiem
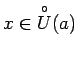 , izpildīsies nevienādība
, izpildīsies nevienādība
Šajā apkārtnē
![]() un funkcija
un funkcija
![]() būs definēta visos funkcijas
būs definēta visos funkcijas ![]() definīcijas apgabala punktos. No
šīs nevienādības iegūsim
definīcijas apgabala punktos. No
šīs nevienādības iegūsim
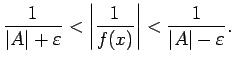
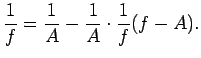
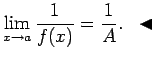
Piemēram,
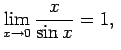 jo
jo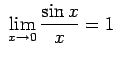 un
un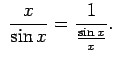
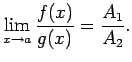
(Pierādīt patstāvīgi, izmantojot 3.13. un
3.12. teorēmas, pie tam
![]() ).
).
Ja