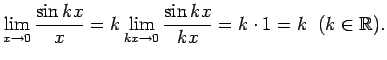Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.7. Teorēmas par nevienādībām
Augstāk: 3. ROBEŽA
Iepriekšējais: 3.5. Teorēmas par funkcijas galīgajām robežām
-
3.15. teorēma.
- Ja eksistē robežas
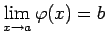 ,
,
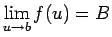 un salikta funkcija
un salikta funkcija
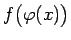 definēta punkta
definēta punkta
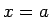 pārdurtā apkārtnē, pie tam šajā apkārtnē
pārdurtā apkārtnē, pie tam šajā apkārtnē
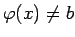 , tad punktā
, tad punktā 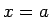 eksistē robeža saliktai funkcijai
eksistē robeža saliktai funkcijai
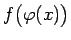 un šī robeža ir
un šī robeža ir 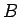 , t.i.,
, t.i.,
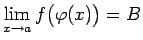 .
.
 Saskaņā ar funkcijas
Saskaņā ar funkcijas  robežas
robežas 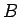 definīciju punkta
definīciju punkta 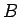 patvaļīgai apkārtnei eksistē punkta
patvaļīgai apkārtnei eksistē punkta 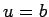 tāda apkārtne
tāda apkārtne
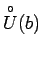 , ka visiem
, ka visiem
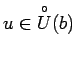 izpildīsies sakarība
izpildīsies sakarība
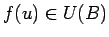 (3.23. zīm.).
(3.23. zīm.).
Saskaņā ar funkcijas 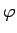 robežas
robežas 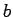 definīciju punkta
definīciju punkta 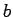 patvaļīgai apkārtnei, tai skaitā, arī iepriekš izvēlētajai
apkārtnei
patvaļīgai apkārtnei, tai skaitā, arī iepriekš izvēlētajai
apkārtnei
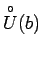 eksistē punkta
eksistē punkta 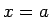 tāda apkārtne
tāda apkārtne
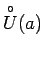 , ka visiem
, ka visiem
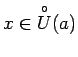 ,
izpildīsies sakarība
,
izpildīsies sakarība
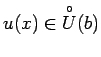 (3.23. zīm.). Apvienojot šos divus apgalvojumus vienā,
var teikt, ka punkta
(3.23. zīm.). Apvienojot šos divus apgalvojumus vienā,
var teikt, ka punkta 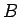 patvaļīgai apkārtnei
patvaļīgai apkārtnei 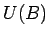 eksistē
punkta
eksistē
punkta 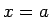 tāda apkārtne
tāda apkārtne
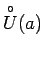 , ka visiem
, ka visiem
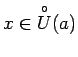 , izpildīsies sakarība
, izpildīsies sakarība
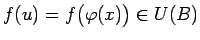 , t.i.,
, t.i.,
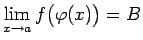 .
.
Piemēram,



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.7. Teorēmas par nevienādībām
Augstāk: 3. ROBEŽA
Iepriekšējais: 3.5. Teorēmas par funkcijas galīgajām robežām
2003-02-24
![]() Saskaņā ar funkcijas
Saskaņā ar funkcijas ![]() robežas
robežas ![]() definīciju punkta
definīciju punkta ![]() patvaļīgai apkārtnei eksistē punkta
patvaļīgai apkārtnei eksistē punkta ![]() tāda apkārtne
tāda apkārtne
![]() , ka visiem
, ka visiem
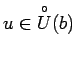 izpildīsies sakarība
izpildīsies sakarība
![]() (3.23. zīm.).
(3.23. zīm.).
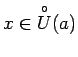 ,
izpildīsies sakarība
,
izpildīsies sakarība
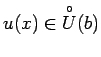 (3.23. zīm.). Apvienojot šos divus apgalvojumus vienā,
var teikt, ka punkta
(3.23. zīm.). Apvienojot šos divus apgalvojumus vienā,
var teikt, ka punkta 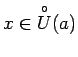 , izpildīsies sakarība
, izpildīsies sakarība