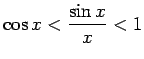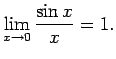Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.8. Funkcijas vienpusējās robežas
Augstāk: 3. ROBEŽA
Iepriekšējais: 3.6. Teorēma par saliktas funkcijas robežu
-
3.16. teorēma.
- Ja funkcijām
 un
un 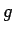 punktā
punktā 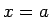 eksistē
robežas, pie tam
eksistē
robežas, pie tam
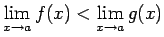 , tad eksistē punkta
, tad eksistē punkta 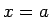 tāda apkārtne, kurā
tāda apkārtne, kurā
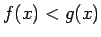 .
.
 Apzīmēsim ar
Apzīmēsim ar
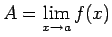 un
un
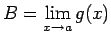 . Pēc dotā
. Pēc dotā 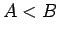 .
Izvēlēsimies šo punktu
.
Izvēlēsimies šo punktu 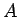 un
un 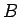 tādas apkārtnes
tādas apkārtnes 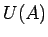 un
un
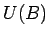 , kas nešķeļas, t.i.,
, kas nešķeļas, t.i.,
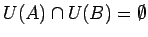 (3.24. zīm.). Saskaņā ar funkcijas
(3.24. zīm.). Saskaņā ar funkcijas  robežas
robežas 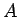 definīciju punkta
definīciju punkta 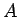 patvaļīgai apkārtnei, tai skaitā, apkārtnei
patvaļīgai apkārtnei, tai skaitā, apkārtnei
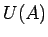 eksistē punkta
eksistē punkta 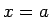 apkārtne
apkārtne
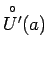 , ka
visiem
, ka
visiem
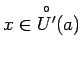 , izpildīsies sakarība
, izpildīsies sakarība
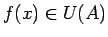 . Līdzīgā veidā apkārtnei
. Līdzīgā veidā apkārtnei 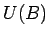 eksistē apkārtne
eksistē apkārtne
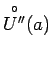 , ka visiem
, ka visiem
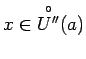 , izpildīsies sakarība
, izpildīsies sakarība
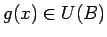 . Apzīmēsim ar
. Apzīmēsim ar
Tagad visiem
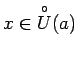 vienlaicīgi
vienlaicīgi
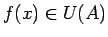 un
un
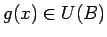 (3.24. zīm.). Tā kā
(3.24. zīm.). Tā kā 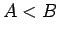 , tad
visiem
, tad
visiem
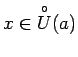 ,
, 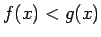 .
.
- Sekas.
- Ja
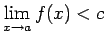 (vai
(vai
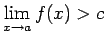 ), tad eksistē punkta
), tad eksistē punkta 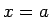 tāda apkārtne, kurā
tāda apkārtne, kurā
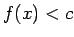 (vai
(vai 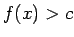 ).
).
(Pierādīt patstāvīgi)
Apskatīsim gadījumu, kad 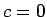 . Šoreiz, ja
. Šoreiz, ja
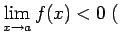
vai
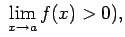
tad eksistē punkta 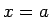 tāda apkārtne, kurā
tāda apkārtne, kurā 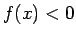 (vai
(vai 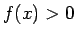 ).
).
-
3.17. teorēma.
- Ja eksistē robežas
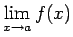 un
un
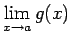 , pie tam
, pie tam
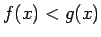 punkta
punkta 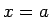 kaut kādā apkārtnē, tad
kaut kādā apkārtnē, tad
(Pierādīt patstāvīgi3.8)
-
3.18. teorēma.
- Ja punktā
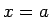 funkcijām
funkcijām  un
un
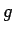 eksistē vienādas robežas, t.i.,
eksistē vienādas robežas, t.i.,
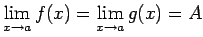 un punkta
un punkta 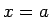 kaut kādā
apkārtnē izpildās nevienādība
kaut kādā
apkārtnē izpildās nevienādība
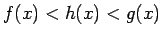 ,
tad punktā
,
tad punktā
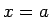 funkcijai
funkcijai 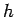 eksistē robeža, pie tam
eksistē robeža, pie tam
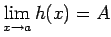 .
.
 Saskaņā ar funkcijas
Saskaņā ar funkcijas  robežas
robežas 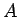 definīciju patvaļīgai punkta
definīciju patvaļīgai punkta 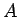 apkārtnei
apkārtnei 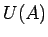 eksistē punkta
eksistē punkta
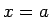 tāda apkārtne
tāda apkārtne
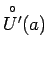 , ka visiem
, ka visiem
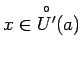 , izpildīsies sakarība
, izpildīsies sakarība
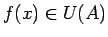 .
Punkts
.
Punkts 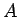 ir par robežu arī funkcijai
ir par robežu arī funkcijai 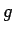 , tāpēc apkārtnei
, tāpēc apkārtnei 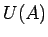 eksistē punkta
eksistē punkta 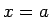 tāda apkārtne
tāda apkārtne
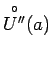 , ka
visiem
, ka
visiem
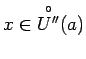 izpildīsies sakarība
izpildīsies sakarība
 . Pēc dotā visiem
. Pēc dotā visiem
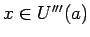 izpildīsies nevienādība
izpildīsies nevienādība
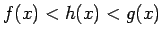 . Apzīmēsim ar
. Apzīmēsim ar
Tagad visiem
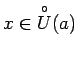 izpildīsies vienlaicīgi
izpildīsies vienlaicīgi
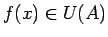 un
un
 . Tā kā
. Tā kā 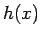 atrodas starp
atrodas starp
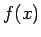 un
un 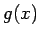 , tad visiem
, tad visiem
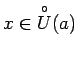
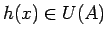 , t.i.,
, t.i.,
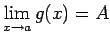 (3.25. zīm.).
(3.25. zīm.).
Piemēram,
punkta 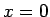 apkārtnē un
apkārtnē un
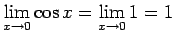 . Tāpēc
. Tāpēc



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.8. Funkcijas vienpusējās robežas
Augstāk: 3. ROBEŽA
Iepriekšējais: 3.6. Teorēma par saliktas funkcijas robežu
2003-02-24
![]() Apzīmēsim ar
Apzīmēsim ar
![]() un
un
![]() . Pēc dotā
. Pēc dotā ![]() .
Izvēlēsimies šo punktu
.
Izvēlēsimies šo punktu ![]() un
un ![]() tādas apkārtnes
tādas apkārtnes ![]() un
un
![]() , kas nešķeļas, t.i.,
, kas nešķeļas, t.i.,
![]() (3.24. zīm.). Saskaņā ar funkcijas
(3.24. zīm.). Saskaņā ar funkcijas ![]() robežas
robežas ![]() definīciju punkta
definīciju punkta ![]() patvaļīgai apkārtnei, tai skaitā, apkārtnei
patvaļīgai apkārtnei, tai skaitā, apkārtnei
![]() eksistē punkta
eksistē punkta ![]() apkārtne
apkārtne
![]() , ka
visiem
, ka
visiem
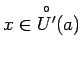 , izpildīsies sakarība
, izpildīsies sakarība
![]() . Līdzīgā veidā apkārtnei
. Līdzīgā veidā apkārtnei ![]() eksistē apkārtne
eksistē apkārtne
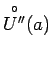 , ka visiem
, ka visiem
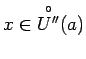 , izpildīsies sakarība
, izpildīsies sakarība
![]() . Apzīmēsim ar
. Apzīmēsim ar
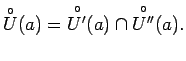
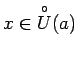 vienlaicīgi
vienlaicīgi
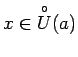 ,
, ![]() Saskaņā ar funkcijas
Saskaņā ar funkcijas ![]() robežas
robežas ![]() definīciju patvaļīgai punkta
definīciju patvaļīgai punkta ![]() apkārtnei
apkārtnei ![]() eksistē punkta
eksistē punkta
![]() tāda apkārtne
tāda apkārtne
![]() , ka visiem
, ka visiem
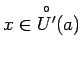 , izpildīsies sakarība
, izpildīsies sakarība
![]() .
Punkts
.
Punkts ![]() ir par robežu arī funkcijai
ir par robežu arī funkcijai ![]() , tāpēc apkārtnei
, tāpēc apkārtnei ![]() eksistē punkta
eksistē punkta ![]() tāda apkārtne
tāda apkārtne
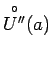 , ka
visiem
, ka
visiem
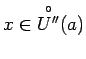 izpildīsies sakarība
izpildīsies sakarība
![]() . Pēc dotā visiem
. Pēc dotā visiem
![]() izpildīsies nevienādība
izpildīsies nevienādība
![]() . Apzīmēsim ar
. Apzīmēsim ar
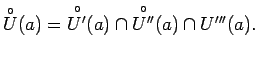
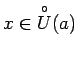 izpildīsies vienlaicīgi
izpildīsies vienlaicīgi