


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.9. Bezgalīgi mazas un bezgalīgi lielas
Augstāk: 3. ROBEŽA
Iepriekšējais: 3.7. Teorēmas par nevienādībām
-
3.7. definīcija.
- Punktu
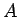 nosauksim par funkcijas
nosauksim par funkcijas  robežu
punktā
robežu
punktā 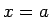 (
(
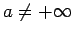 ) no labās puses, ja punkta
) no labās puses, ja punkta 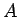 patvaļīgai apkārtnei
patvaļīgai apkārtnei 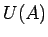 eksistē punkta
eksistē punkta 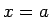 tāda apkārtne
tāda apkārtne
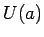 , ka visiem
, ka visiem 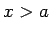 un
un 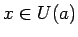 izpildīsies sakarība
izpildīsies sakarība
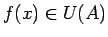 (3.26. zīm.).
(3.26. zīm.).
Apzīmēsim
Analoģiski var definēt funkcijas robežu punktā no kreisās puses.
Šo robežu apzīmēsim
Acīmredzami, ir spēkā šādi apgalvojumi:
- Ja
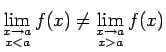 , tad
, tad
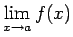 -
neeksistē;
-
neeksistē;
-
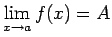 tad un tikai tad,
kad
tad un tikai tad,
kad
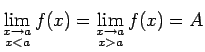 .
.
Piemēram, funkcijai
(skat.3.9)
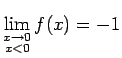 , bet
, bet
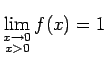 , tāpēc
, tāpēc
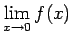 - neeksistē
(3.27. zīm.).
- neeksistē
(3.27. zīm.).



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.9. Bezgalīgi mazas un bezgalīgi lielas
Augstāk: 3. ROBEŽA
Iepriekšējais: 3.7. Teorēmas par nevienādībām
2003-02-24
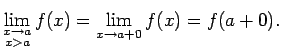
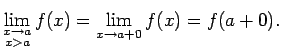
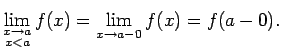
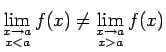 , tad
, tad
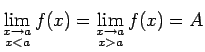 .
.
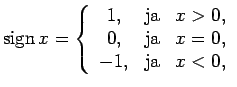
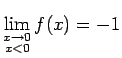 , bet
, bet
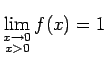 , tāpēc
, tāpēc