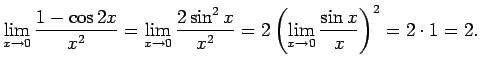Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.10. Monotonas virknes robeža
Augstāk: 3. ROBEŽA
Iepriekšējais: 3.8. Funkcijas vienpusējās robežas
-
3.8. definīcija.
- Funkciju
 nosauksim par bezgalīgi mazu
funkciju3.10, kad
nosauksim par bezgalīgi mazu
funkciju3.10, kad  tiecas uz
tiecas uz  , ja
, ja
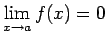 .
.
Piemēram, 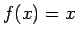 ir bezgalīgi maza funkcija, kad
ir bezgalīgi maza funkcija, kad  tiecas uz
nulli, jo
tiecas uz
nulli, jo
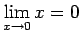 .
.
-
3.9. definīcija.
- Funkciju
 nosauksim par bezgalīgi lielu
funkciju, kad
nosauksim par bezgalīgi lielu
funkciju, kad  tiecas uz
tiecas uz  , ja
, ja
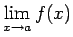 ir bezgalība.
ir bezgalība.
Piemēram,
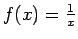 ir bezgalīgi liela funkcija, kad
ir bezgalīgi liela funkcija, kad  tiecas uz nulli.
tiecas uz nulli.
-
3.19. teorēma.
- Ja
 ir bezgalīgi maza funkcija, kad
ir bezgalīgi maza funkcija, kad  tiecas
uz
tiecas
uz  , tad
, tad
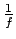 - bezgalīgi liela funkcija, kad
- bezgalīgi liela funkcija, kad  tiecas uz
tiecas uz  .
.
 Tā kā
Tā kā  ir bezgalīgi maza funkcija, kad
ir bezgalīgi maza funkcija, kad
 tiecas uz
tiecas uz  , tad
, tad
Saskaņā ar robežas definīciju jebkuram
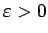 eksistē
punkta
eksistē
punkta 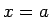 tāda apkārtne
tāda apkārtne
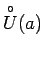 , ka visiem
, ka visiem
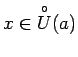 izpildīsies nevienādība
izpildīsies nevienādība
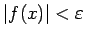 . Seko, ka
Tātad
. Seko, ka
Tātad
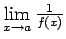 ir bezgalība,
t.i.,
ir bezgalība,
t.i.,
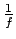 - bezgalīgi liela funkcija, kad
- bezgalīgi liela funkcija, kad  tiecas uz
tiecas uz
 .
.
Acīmredzami, 3.19. teorēmai apgrieztais apgalvojums arī
ir spēkā.
Apskatīsim divas bezgalīgi mazas funkcijas 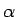 un
un 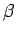 ,
kad
,
kad  tiecas uz
tiecas uz  . Apzīmēsim ar
. Apzīmēsim ar 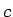 šo funkciju attiecības
šo funkciju attiecības
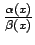 robežu punktā
robežu punktā  , t.i.,
, t.i.,
- Ja
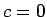 , tad
, tad 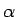 nosauksim par augstākas kārtas
bezgalīgi mazu funkciju, salīdzinot ar
nosauksim par augstākas kārtas
bezgalīgi mazu funkciju, salīdzinot ar 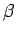 , kad
, kad  tiecas
uz
tiecas
uz  un pierakstīsim
un pierakstīsim
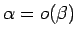 (skat.3.11).
(skat.3.11).
- Ja
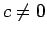 (
(
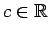 ), tad
), tad 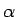 ,
, 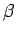 nosauksim
par vienādas kārtas
bezgalīgi mazām funkcijām, kad
nosauksim
par vienādas kārtas
bezgalīgi mazām funkcijām, kad  tiecas
uz
tiecas
uz  .
.
- Īpaši izdalīsim gadījumu, kad
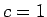 , t.i.,
Šoreiz
, t.i.,
Šoreiz 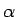 un
un 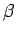 nosauksim par
ekvivalentām3.12 bezgalīgi mazām funkcijām, kad
nosauksim par
ekvivalentām3.12 bezgalīgi mazām funkcijām, kad  tiecas uz
tiecas uz  .
Pierakstīsim
.
Pierakstīsim
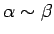 (
(
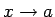 ). Piemēram,
). Piemēram,
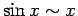 (
(
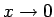 ), jo
), jo
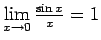 .
.
-
3.20. teorēma.
- Ja
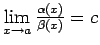 ,
,
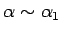 (
(
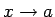 ) un
) un
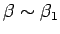 (
(
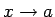 ), tad
), tad
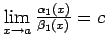 .
.
Apgalvojums kļūst acīmredzams, ja
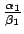 uzraksta šādi:
uzraksta šādi:
3.20. teorēmu plaši pielieto robežu aprēķināšanā,
t.i., funkcijas aizstāj ar tām ekvivalentām bezgalīgi mazām
funkcijām, kad  tiecas uz
tiecas uz  .
.
-
3.10. definīcija.
- Funkciju
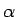 nosauksim par
nosauksim par 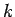 -tās kārtas
bezgalīgi mazu funkciju, salīdzinot ar bezgalīgi mazu funkciju
-tās kārtas
bezgalīgi mazu funkciju, salīdzinot ar bezgalīgi mazu funkciju
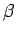 , kad
, kad  tiecas uz
tiecas uz  , ja
, ja 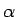 un
un 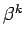 (
(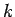 - naturāls
skaitlis) ir vienādas kārtas bezgalīgi mazas funkcijas, kad
- naturāls
skaitlis) ir vienādas kārtas bezgalīgi mazas funkcijas, kad  tiecas uz
tiecas uz  .
.
Piemēram, funkcija
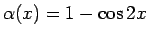 ir 2. kārtas bezgalīgi
maza funkcija, kad
ir 2. kārtas bezgalīgi
maza funkcija, kad
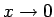 , salīdzinot ar funkciju
, salīdzinot ar funkciju
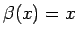 , jo
, jo



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.10. Monotonas virknes robeža
Augstāk: 3. ROBEŽA
Iepriekšējais: 3.8. Funkcijas vienpusējās robežas
2003-02-24
![]() ir bezgalīgi maza funkcija, kad
ir bezgalīgi maza funkcija, kad ![]() tiecas uz
nulli, jo
tiecas uz
nulli, jo
![]() .
.
![]() ir bezgalīgi liela funkcija, kad
ir bezgalīgi liela funkcija, kad ![]() tiecas uz nulli.
tiecas uz nulli.
![]() Tā kā
Tā kā ![]() ir bezgalīgi maza funkcija, kad
ir bezgalīgi maza funkcija, kad
![]() tiecas uz
tiecas uz ![]() , tad
, tad
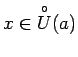 izpildīsies nevienādība
izpildīsies nevienādība
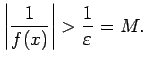
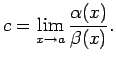
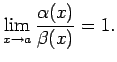
![]() uzraksta šādi:
uzraksta šādi:
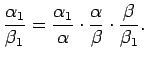
![]() tiecas uz
tiecas uz ![]() .
.
![]() ir 2. kārtas bezgalīgi
maza funkcija, kad
ir 2. kārtas bezgalīgi
maza funkcija, kad
![]() , salīdzinot ar funkciju
, salīdzinot ar funkciju
![]() , jo
, jo