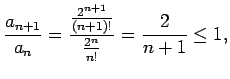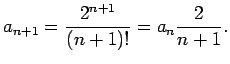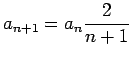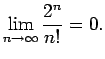Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.11. Skaitlis e
Augstāk: 3. ROBEŽA
Iepriekšējais: 3.9. Bezgalīgi mazas un bezgalīgi lielas
-
3.11. definīcija.
- Skaitļu virkni
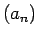 nosauksim par augošu (vai
dilstošu), ja
nosauksim par augošu (vai
dilstošu), ja
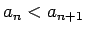 (
(
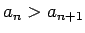 ), kur
), kur  - naturāls
skaitlis.
- naturāls
skaitlis.
-
3.12. definīcija.
- Skaitļu virkni
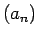 nosauksim par nedilstošu
(vai neaugošu), ja
nosauksim par nedilstošu
(vai neaugošu), ja
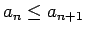 (vai
(vai
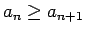 ), kur
), kur
 - naturāls skaitlis.
- naturāls skaitlis.
-
3.13. definīcija.
- Skaitļu virkni (
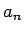 ) nosauksim par ierobežotu
no augšas (vai ierobežotu no apakšas), ja ir ierobežota no
augšas (vai ierobežota no apakšas) tās vērtību kopa.
) nosauksim par ierobežotu
no augšas (vai ierobežotu no apakšas), ja ir ierobežota no
augšas (vai ierobežota no apakšas) tās vērtību kopa.
-
3.14. definīcija.
- Par skaitļu virknes (
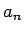 ) augšējo slieksni (vai apakšējo
slieksni) nosauksim šīs virknes vērtību kopas augšējo slieksni
(vai apakšējo slieksni).
) augšējo slieksni (vai apakšējo
slieksni) nosauksim šīs virknes vērtību kopas augšējo slieksni
(vai apakšējo slieksni).
Šos sliekšņus apzīmēsim
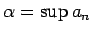 ,
,
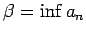 .
.
-
3.21. teorēma.
- Katra augoša un ierobežota no
augšas virkne ir konverģenta.
 Tā kā virkne (
Tā kā virkne (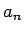 ) ir ierobežota no
augšas, tad tai eksistē galīgs augšējais slieksnis
) ir ierobežota no
augšas, tad tai eksistē galīgs augšējais slieksnis
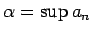 . Parādīsim, ka eksistē robeža
. Parādīsim, ka eksistē robeža
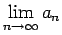 un tā ir vienāda ar
un tā ir vienāda ar
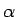 .
.
Saskaņā ar kopas augšējā sliekšņa
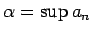 definīciju var
teikt, ka
definīciju var
teikt, ka
-
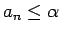 (
( - naturāls skaitlis);
- naturāls skaitlis);
- jebkuram
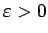 eksistē
tāds
eksistē
tāds 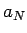 , ka
, ka
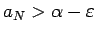 .
.
Tā kā virkne (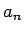 ) augoša, tad visiem tās numuriem
) augoša, tad visiem tās numuriem 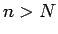 izpildīsies nevienādība
izpildīsies nevienādība
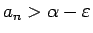 .
.
Visiem numuriem  , tai skaitā arī
, tai skaitā arī 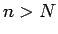 , izpildīsies nevienādība
, izpildīsies nevienādība
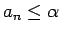 . Iegūsim, ka visiem
. Iegūsim, ka visiem 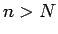 , izpildīsies divkārša
nevienādība
, izpildīsies divkārša
nevienādība
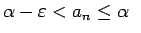
vai
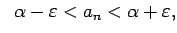
t.i., virkne
(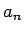 ) konverģenta un
) konverģenta un
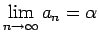 .
.
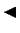
Analoģiski pierāda, ka ir konverģenta katra dilstoša un ierobežota
no apakšas virkne. Šoreiz
- Sekas.
- Konverģentai un augošai virknei (
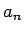 ) izpildās
nevienādība
) izpildās
nevienādība
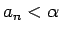 , kur
, kur
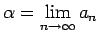 (
( - naturāls
skaitlis).
- naturāls
skaitlis).
 Saskaņā ar 3.21. teorēmu visiem
numuriem
Saskaņā ar 3.21. teorēmu visiem
numuriem 
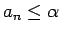 . Ja pieņemtu, ka kādam numuram
. Ja pieņemtu, ka kādam numuram 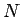
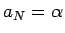 , tad
, tad
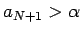 , jo virkne augoša. Radās
pretruna.
, jo virkne augoša. Radās
pretruna.
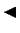
Ilustrēsim šo teorēmu ar konkrētu piemēru. Apskatīsim virkni
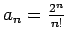 . Apskatīsim attiecību
tas nozīmē, ka virkne ir neaugoša un, acīmredzami, ierobežota no
apakšas, piemēram, ar nulli. Tātad virkne (
. Apskatīsim attiecību
tas nozīmē, ka virkne ir neaugoša un, acīmredzami, ierobežota no
apakšas, piemēram, ar nulli. Tātad virkne (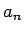 ) ir konverģenta.
Tās robežu apzīmēsim ar
) ir konverģenta.
Tās robežu apzīmēsim ar
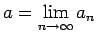 . Atradīsim šo robežu
. Atradīsim šo robežu  .
Vienādībā
pāriesim pie robežas, kad
.
Vienādībā
pāriesim pie robežas, kad  tiecas uz bezgalību. Iegūsim, ka
tiecas uz bezgalību. Iegūsim, ka
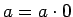 , t.i.,
, t.i., 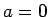 . Tātad
Esam ne
tikai pierādījuši virknes (
. Tātad
Esam ne
tikai pierādījuši virknes (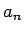 ) konverģenci, bet arī
izskaitļojuši tās robežu.
) konverģenci, bet arī
izskaitļojuši tās robežu.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.11. Skaitlis e
Augstāk: 3. ROBEŽA
Iepriekšējais: 3.9. Bezgalīgi mazas un bezgalīgi lielas
2003-02-24
![]() Tā kā virkne (
Tā kā virkne (![]() ) ir ierobežota no
augšas, tad tai eksistē galīgs augšējais slieksnis
) ir ierobežota no
augšas, tad tai eksistē galīgs augšējais slieksnis
![]() . Parādīsim, ka eksistē robeža
. Parādīsim, ka eksistē robeža
![]() un tā ir vienāda ar
un tā ir vienāda ar
![]() .
.
![]() ) augoša, tad visiem tās numuriem
) augoša, tad visiem tās numuriem ![]() izpildīsies nevienādība
izpildīsies nevienādība
![]() .
.
![]() Saskaņā ar 3.21. teorēmu visiem
numuriem
Saskaņā ar 3.21. teorēmu visiem
numuriem ![]()
![]() . Ja pieņemtu, ka kādam numuram
. Ja pieņemtu, ka kādam numuram ![]()
![]() , tad
, tad
![]() , jo virkne augoša. Radās
pretruna.
, jo virkne augoša. Radās
pretruna.
![]()