


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.12. Savelkošos slēgtu intervālu princips
Augstāk: 3. ROBEŽA
Iepriekšējais: 3.10. Monotonas virknes robeža
-
3.22. teorēma.
- Funkcijai
punktā
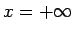 eksistē
galīga robeža, kuru apzīmē ar
eksistē
galīga robeža, kuru apzīmē ar 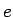 .
.
 Vispirms apskatīsim virkni
Vispirms apskatīsim virkni
un parādīsim, ka tā konverģē. Apskatīsim attiecību
Saskaņā ar Bernulli nevienādību
tāpēc
Esam ieguvuši, ka
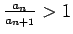 , t.i.,
, t.i.,
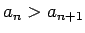 .
Seko, ka virkne (
.
Seko, ka virkne (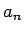 ) ir dilstoša un, acīmredzami, ierobežota no
apakšas, piemēram, ar nulli. Virkne (
) ir dilstoša un, acīmredzami, ierobežota no
apakšas, piemēram, ar nulli. Virkne (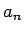 ) konverģē; tās robežu
apzīmēsim ar
Saskaņā ar Bernulli nevienādību
Viegli izskaitļot un pārliecināties, ka
) konverģē; tās robežu
apzīmēsim ar
Saskaņā ar Bernulli nevienādību
Viegli izskaitļot un pārliecināties, ka 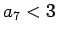 . Tā kā virkne
(
. Tā kā virkne
(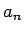 ) ir dilstoša, tad visiem nākamajiem numuriem
) ir dilstoša, tad visiem nākamajiem numuriem 
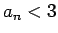 .
Virknes robeža
.
Virknes robeža 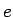 atradīsies intervālā
atradīsies intervālā 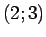 , t.i.,
, t.i., 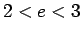 .
.
Tā kā skaitļa  veselā sastāvdaļa
veselā sastāvdaļa ![$ [x]$](img756.gif) apmierina nevienādību
tad, acīmredzami, izpildīsies arī nevienādība
apmierina nevienādību
tad, acīmredzami, izpildīsies arī nevienādība
Ja  tiecas uz
tiecas uz 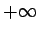 , tad
, tad ![$ [x]$](img756.gif) diskrēti3.13 tiecas uz
diskrēti3.13 tiecas uz 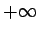 . Saskaņā
ar iepriekš apskatīto gadījumu robeža no nevienādības (*) labās
puses ir
. Saskaņā
ar iepriekš apskatīto gadījumu robeža no nevienādības (*) labās
puses ir 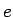 , t.i.,
, t.i.,
Parādīsim, ka robeža no nevienādības kreisās puses arī ir 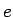 ,
Šīs vienādības labās puses
pirmajam loceklim robeža ir
,
Šīs vienādības labās puses
pirmajam loceklim robeža ir 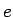 , t.i.,
bet otrajam loceklim robeža ir viens, t.i.,
tāpēc
, t.i.,
bet otrajam loceklim robeža ir viens, t.i.,
tāpēc
Saskaņā ar 3.18. teorēmu eksistē robeža
Parādīsim, ka funkcijai
punktā 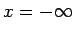 eksistē robeža, kas arī ir skaitlis
eksistē robeža, kas arī ir skaitlis 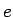 .
.
Pārveidosim
Ja  tiecas uz
tiecas uz 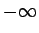 , tad
, tad 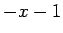 tiecas uz
tiecas uz 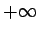 . Robeža
šīs vienādības labajai pusei ir
. Robeža
šīs vienādības labajai pusei ir
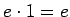 . Tātad arī kreisajai
pusei robeža eksistē un ir vienāda ar
. Tātad arī kreisajai
pusei robeža eksistē un ir vienāda ar 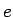 , t.i.,
Turpmāk rakstīsim
Viegli saskatīt, ka
, t.i.,
Turpmāk rakstīsim
Viegli saskatīt, ka
Skaitļa 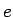 vērtība ar 26 zīmēm pēc komata ir
vērtība ar 26 zīmēm pēc komata ir



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.12. Savelkošos slēgtu intervālu princips
Augstāk: 3. ROBEŽA
Iepriekšējais: 3.10. Monotonas virknes robeža
2003-02-24
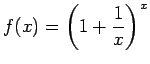
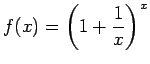
![]() Vispirms apskatīsim virkni
Vispirms apskatīsim virkni
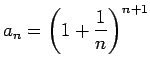
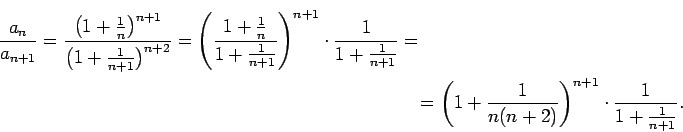
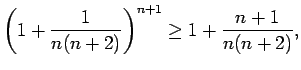
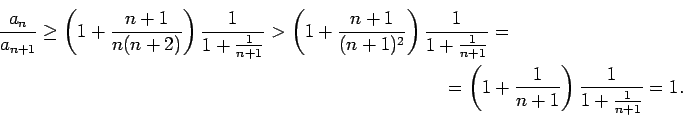
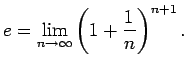
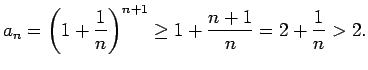
![$\displaystyle \left(1+\frac{1}{[x]+1}\right)^{[x]}<\left(1+\frac{1}{x}\right)^x<
\left(1+\frac{1}{[x]}\right)^{[x]+1}\/.\eqno{(*)}$](img758.gif)
![]() tiecas uz
tiecas uz ![]() , tad
, tad ![]() diskrēti3.13 tiecas uz
diskrēti3.13 tiecas uz ![]() . Saskaņā
ar iepriekš apskatīto gadījumu robeža no nevienādības (*) labās
puses ir
. Saskaņā
ar iepriekš apskatīto gadījumu robeža no nevienādības (*) labās
puses ir ![]() , t.i.,
, t.i.,
![$\displaystyle \lim\limits_{x\rightarrow+\infty}\left(1+\frac{1}{[x]}\right)^{[x]+1}=e\/.$](img759.gif)
![$\displaystyle \left(1+\frac{1}{[x]+1}\right)^{[x]}=\left(1+\frac{1}{[x]+1}\right)^{[x]+2}:
\left(1+\frac{1}{[x]+1}\right)^2\/.$](img760.gif)
![$\displaystyle \lim\limits_{x\rightarrow+\infty}\left(1+\frac{1}{[x]+1}\right)^{[x]+2}=e\/,$](img761.gif)
![$\displaystyle \lim\limits_{x\rightarrow+\infty}\left(1+\frac{1}{[x]+1}\right)^{2}=1\/,$](img762.gif)
![$\displaystyle \lim\limits_{x\rightarrow+\infty}\left(1+\frac{1}{[x]+1}\right)^{[x]}=e:1=e\/.$](img763.gif)
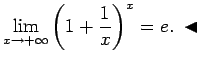
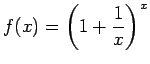
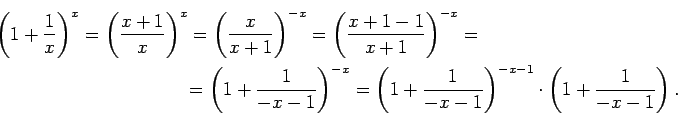
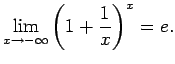
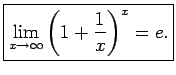
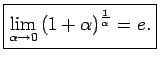
![]() vērtība ar 26 zīmēm pēc komata ir
vērtība ar 26 zīmēm pēc komata ir