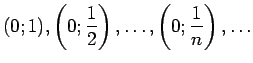Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.13. Bolcano-Veierštrāsa teorēma
Augstāk: 3. ROBEŽA
Iepriekšējais: 3.11. Skaitlis e
-
3.15. definīcija.
- Slēgtu intervālu virkni
![$ \bigl([a_n;b_n]\bigr)$](img773.gif) sauksim par savelkošos slēgtu intervālu virkni, ja
sauksim par savelkošos slēgtu intervālu virkni, ja
-
![$ [a_1;b_1]\supset[a_2;b_2]\supset\cdots\supset[a_n;b_n]\supset\cdots$](img160.gif) ;
;
-
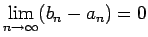 .
.
-
3.23. teorēma.
- Savelkošos slēgtu intervālu
virknei
![$ \bigl([a_n;b_n]\bigr)$](img773.gif) eksistē vienīgs kopīgs punkts.
eksistē vienīgs kopīgs punkts.
 Izveidosim virkni
Izveidosim virkni 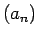 . Šī virkne,
acīmredzami, ir nedilstoša un ierobežota no augšas,
piemēram, ar
. Šī virkne,
acīmredzami, ir nedilstoša un ierobežota no augšas,
piemēram, ar 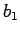 . Eksistē galīga robeža
. Eksistē galīga robeža
Otra virkne 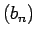 ir neaugoša un ierobežota no apakšas, tāpēc
eksistē galīga robeža
Tā kā
ir neaugoša un ierobežota no apakšas, tāpēc
eksistē galīga robeža
Tā kā
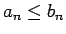 , tad
t.i.,
, tad
t.i.,
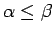 . Saskaņā ar kopas sliekšņu definīcijām
. Saskaņā ar kopas sliekšņu definīcijām
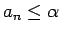 ,
,
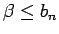 . Tāpēc izpildīsies nevienādība
. Tāpēc izpildīsies nevienādība
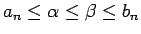 . No šīs nevienādības seko, ka
. No šīs nevienādības seko, ka
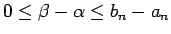 . Robeža no šīs nevienādības
kreisās un labās puses ir nulle, tāpēc arī robeža no konstantes
. Robeža no šīs nevienādības
kreisās un labās puses ir nulle, tāpēc arī robeža no konstantes
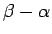 arī ir nulle, t.i.,
Robeža no konstantes ir vienāda ar šo konstanti, tāpēc seko, ka
arī ir nulle, t.i.,
Robeža no konstantes ir vienāda ar šo konstanti, tāpēc seko, ka
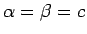 . Esam ieguvuši nevienādību
. Esam ieguvuši nevienādību
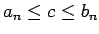 ,
t.i., eksistē skaitlis
,
t.i., eksistē skaitlis 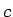 , kopīgs visiem slēgtajiem intervāliem
, kopīgs visiem slēgtajiem intervāliem
![$ [a_n;b_n]$](img785.gif) . Te arī tika pierādīts šāda kopīga skaitļa
. Te arī tika pierādīts šāda kopīga skaitļa 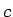 vienīgums.
vienīgums.
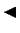
Vaļēju intervālu virknei šī teorēma nav spēkā, piemēram, virknei
nav kopīgā punkta. Teorēma būs spēkā tikai tādai vaļēju intervālu
virknei, kura katrs nākamais vaļējais intervāls stingri iekļaujas
iepriekšējā, t.i.,
( - naturāls skaitlis) un kurai
- naturāls skaitlis) un kurai
Savelkošos slēgtu intervālu principu varētu ņemt par reālu skaitļu
kopas nepārtrauktības aksiomu.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.13. Bolcano-Veierštrāsa teorēma
Augstāk: 3. ROBEŽA
Iepriekšējais: 3.11. Skaitlis e
2003-02-24
![$ [a_1;b_1]\supset[a_2;b_2]\supset\cdots\supset[a_n;b_n]\supset\cdots$](img160.gif) ;
;
 .
.
![]() Izveidosim virkni
Izveidosim virkni ![]() . Šī virkne,
acīmredzami, ir nedilstoša un ierobežota no augšas,
piemēram, ar
. Šī virkne,
acīmredzami, ir nedilstoša un ierobežota no augšas,
piemēram, ar ![]() . Eksistē galīga robeža
. Eksistē galīga robeža