


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.14. Skaitļu virknes konverģences Košī kritērijs
Augstāk: 3. ROBEŽA
Iepriekšējais: 3.12. Savelkošos slēgtu intervālu princips
-
3.24. teorēma.
- [Bolcano
3.14-
Veierštrāsa3.15 teorēma]
No jebkuras ierobežotas skaitļu virknes var izdalīt
konverģentu apakšvirkni.
 Vispirms pierādīsim, ka no jebkuras skaitļu
virknes
Vispirms pierādīsim, ka no jebkuras skaitļu
virknes 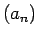 var izdalīt monotonu apakšvirkni.
var izdalīt monotonu apakšvirkni.
Apzīmēsim ar  kopu, kas izveidota no tiem virknes
kopu, kas izveidota no tiem virknes 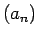 locekļu numuriem, kuriem izpildās šāda prasība: ja
locekļu numuriem, kuriem izpildās šāda prasība: ja 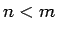 , tad
, tad
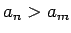 . Iespējami divi gadījumi:
. Iespējami divi gadījumi:
 - bezgalīga kopa. Kopas
- bezgalīga kopa. Kopas  elementiem
atbilst dotās virknes dilstoša apakšvirkne
elementiem
atbilst dotās virknes dilstoša apakšvirkne 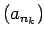 , jo tās
locekļi apmierina sakarību:
(skat. kopas
, jo tās
locekļi apmierina sakarību:
(skat. kopas  konstrukciju).
konstrukciju).
 - galīga kopa. Tātad patvaļīgam
- galīga kopa. Tātad patvaļīgam 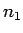 eksistē tāds
numurs
eksistē tāds
numurs 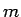 , kur
, kur
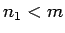 , ka
, ka
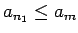 . Vismazāko starp
šādiem numuriem
. Vismazāko starp
šādiem numuriem 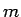 apzīmēsim ar
apzīmēsim ar 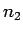 . Esam ieguvuši, ka
. Esam ieguvuši, ka
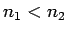 un atbilstoši
un atbilstoši
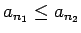 . Ar
. Ar 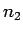 rīkosimies tāpat kā ar
rīkosimies tāpat kā ar 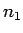 un iegūsim, ka
un iegūsim, ka 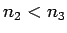 un
atbilstoši
un
atbilstoši
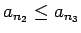 utt. Bezgalīgi turpinot šo
procesu, iegūsim dotās virknes nedilstošu apakšvirkni
utt. Bezgalīgi turpinot šo
procesu, iegūsim dotās virknes nedilstošu apakšvirkni
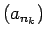 .
.
Tātad abos iespējamos gadījumos no dotās virknes 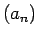 esam
izdalījuši monotonu apakšvirkni
esam
izdalījuši monotonu apakšvirkni
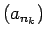 .
.
Dotā virkne ir ierobežota, tāpēc ir ierobežota arī tās apakšvirkne
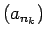 . Zināms, ka katra ierobežota un monotona
virkne ir konverģenta, tāpēc virkne
. Zināms, ka katra ierobežota un monotona
virkne ir konverģenta, tāpēc virkne
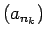 konverģē.
konverģē.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.14. Skaitļu virknes konverģences Košī kritērijs
Augstāk: 3. ROBEŽA
Iepriekšējais: 3.12. Savelkošos slēgtu intervālu princips
2003-02-24
![]() Vispirms pierādīsim, ka no jebkuras skaitļu
virknes
Vispirms pierādīsim, ka no jebkuras skaitļu
virknes ![]() var izdalīt monotonu apakšvirkni.
var izdalīt monotonu apakšvirkni.
![]() esam
izdalījuši monotonu apakšvirkni
esam
izdalījuši monotonu apakšvirkni
![]() .
.