


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.15. Jautājumi
Augstāk: 3. ROBEŽA
Iepriekšējais: 3.13. Bolcano-Veierštrāsa teorēma
-
3.25. teorēma.
- [Košī3.16 kritērijs]
Lai skaitļu virkne 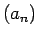 būtu
konverģenta, nepieciešami un pietiekami, lai jebkuram
būtu
konverģenta, nepieciešami un pietiekami, lai jebkuram
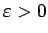 eksistē tāds naturāls skaitlis
eksistē tāds naturāls skaitlis
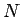 (atkarīgs no
(atkarīgs no
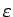 ), ka visiem numuriem
), ka visiem numuriem  ,
, 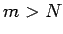 izpildās nevienādība
izpildās nevienādība
 Nepieciešamība. Tā kā
virkne
Nepieciešamība. Tā kā
virkne 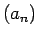 konverģē, tad eksistē galīga robeža
konverģē, tad eksistē galīga robeža
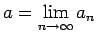 ; saskaņā ar virknes
; saskaņā ar virknes
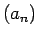 robežas
robežas  definīciju jebkuram
definīciju jebkuram
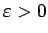 eksistē
tāds naturāls skaitlis, ka visiem
eksistē
tāds naturāls skaitlis, ka visiem 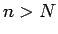 izpildīsies nevienādība
izpildīsies nevienādība
Izvēlēsimies vēl 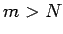 . Šādiem
. Šādiem 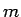 izpildīsies nevienādība
Apskatīsim
Tātad
visiem
izpildīsies nevienādība
Apskatīsim
Tātad
visiem 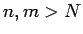 izpildīsies nevienādība
izpildīsies nevienādība
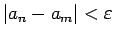 .
.
Pietiekamība. Dots, ka jebkuram
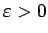 eksistē tāds naturāls skaitlis
eksistē tāds naturāls skaitlis 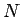 , ka visiem
, ka visiem 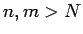 izpildīsies nevienādība
Šī sakarība ir līdzvērtīga nevienādībai
Ja
izpildīsies nevienādība
Šī sakarība ir līdzvērtīga nevienādībai
Ja 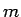 - fiksēts, tad šī
nevienādība norāda, ka virkne
- fiksēts, tad šī
nevienādība norāda, ka virkne 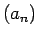 ierobežota. Saskaņā ar
Bolcano-Veierštrāsa teorēmu no šīs virknes var
izdalīt konverģentu apakšvirkni
ierobežota. Saskaņā ar
Bolcano-Veierštrāsa teorēmu no šīs virknes var
izdalīt konverģentu apakšvirkni
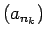 .
Apzīmēsim ar
.
Apzīmēsim ar
Skaitli 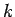 paņemsim tik lielu, lai
paņemsim tik lielu, lai 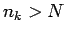 . Tāpēc izpildīsies
nevienādība
. Tāpēc izpildīsies
nevienādība
Šajā nevienādībā pāriesim pie robežas, kad 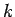 tiecas uz
bezgalību. Iegūsim nevienādību
jeb
Tātad visiem
tiecas uz
bezgalību. Iegūsim nevienādību
jeb
Tātad visiem 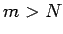 izpildīsies nevienādība
izpildīsies nevienādība
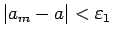 , kur
, kur
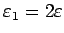 (arī ir
pozitīvs skaitlis). Tas nozīmē, ka dotā virkne ir
konverģenta.
(arī ir
pozitīvs skaitlis). Tas nozīmē, ka dotā virkne ir
konverģenta.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.15. Jautājumi
Augstāk: 3. ROBEŽA
Iepriekšējais: 3.13. Bolcano-Veierštrāsa teorēma
2003-02-24
![]() Nepieciešamība. Tā kā
virkne
Nepieciešamība. Tā kā
virkne ![]() konverģē, tad eksistē galīga robeža
konverģē, tad eksistē galīga robeža
![]() ; saskaņā ar virknes
; saskaņā ar virknes
![]() robežas
robežas ![]() definīciju jebkuram
definīciju jebkuram
![]() eksistē
tāds naturāls skaitlis, ka visiem
eksistē
tāds naturāls skaitlis, ka visiem ![]() izpildīsies nevienādība
izpildīsies nevienādība
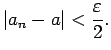
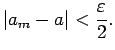
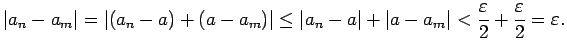
![]() paņemsim tik lielu, lai
paņemsim tik lielu, lai ![]() . Tāpēc izpildīsies
nevienādība
. Tāpēc izpildīsies
nevienādība