


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.16. Vingrinājumi
Augstāk: 3.14. Skaitļu virknes konverģences Košī kritērijs
Iepriekšējais: 3.14. Skaitļu virknes konverģences Košī kritērijs
- Definēt konverģentu skaitļu virkni un tās robežu.
- Uzrakstīt Bernulli nevienādību.
- Definēt diverģentas uz
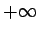 un uz
un uz 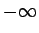 skaitļu
virknes.
skaitļu
virknes.
- Definēt funkcijas robežu punktā (funkcijas robežas vispārīgā
definīcija).
- Definēt vienu no funkcijas galīgām robežām (iespējami 4
gadījumi).
- Definēt vienu no funkcijas bezgalīgām robežām (iespējami 12
gadījumi).
- Formulēt teorēmu par konverģentas virknes ierobežotību.
- Formulēt teorēmu par sinusa attiecības pret argumentu
robežu.
- Formulēt teorēmas par funkcijas galīgām robežām (funkcijas
ierobežotība; konstantas funkcijas robeža; funkcijas moduļa un
reizinājuma ar skaitli robeža; funkciju summas, reizinājuma un dalījuma
robeža).
- Formulēt teorēmu par saliktas funkcijas robežu.
- Formulēt teorēmas par nevienādībām (pāreja pie robežas nevienādības,
mainīga starplieluma
robeža).
- Definēt funkcijas robežu punktā no labās un no kreisās
puses.
- Definēt bezgalīgi mazu un bezgalīgi lielu funkciju.
- Sniegt bezgalīgi mazu funkciju salīdzināšanas
paņēmienus.
- Definēt augošu, dilstošu, neaugošu un nedilstošu skaitļu
virkni.
- Definēt ierobežotu skaitļu virkni.
- Definēt skaitļu virknes augšējo un apakšējo slieksni.
- Formulēt teorēmu par monotonas virknes konverģenci.
- Definēt skaitli ``
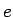 ''.
''.
- Definēt savelkošos slēgtu intervālu virkni.
- Formulēt savelkošos slēgtu intervālu principu.
- Formulēt Bolcano-Veierštrāsa teorēmu par ierobežotas
skaitļu virknes apakšvirkni.
- Formulēt skaitļu virknes konverģences Košī kritēriju.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.16. Vingrinājumi
Augstāk: 3.14. Skaitļu virknes konverģences Košī kritērijs
Iepriekšējais: 3.14. Skaitļu virknes konverģences Košī kritērijs
2003-02-24
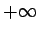 un uz
un uz 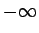 skaitļu
virknes.
skaitļu
virknes.
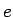 ''.
''.