


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4. FUNKCIJAS NEPĀRTRAUKTĪBA
Augstāk: 3.14. Skaitļu virknes konverģences Košī kritērijs
Iepriekšējais: 3.15. Jautājumi
- Konstruēt konverģentu skaitļu virkni un sniegt tās
robežas ģeometrisku interpretāciju.
- Konstruēt ierobežotu un diverģentu skaitļu virkni.
- Pierādīt, ka Dirihlē funkcijai
neeksistē robeža punktā
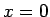 .
.
- Formulēt funkcijas robežas
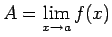 definīciju šādos gadījumos:
definīciju šādos gadījumos:
-
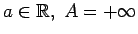 ;
;
-
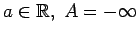 ;
;
-
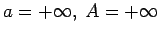 ;
;
-
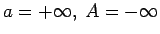 ;
;
-
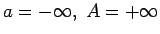 ;
;
-
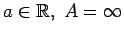 ;
;
-
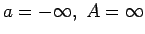 ;
;
-
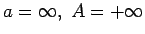 ;
;
-
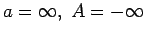 ;
;
-
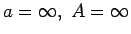 .
.
- Izskaitļot
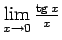 .
.
- Parādīt, ka 3.7. teorēmai apgrieztais
apgalvojums nav spēkā.
- Pierādīt 3.8. teorēmu.
- Parādīt, ka 3.12. teorēmai apgrieztais
apgalvojums nav spēkā.
- Pierādīt 3.14. teorēmu.
- Izskaitļot
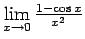 .
.
- Formulēt un pierādīt šādas teorēmas par virknes
galīgām robežām:
- par virknes robežas vienīgumu;
- par divu konverģentu virkņu summu;
- par konverģentas virknes reizinājumu ar skaitli;
- par divu konverģentu virkņu reizinājumu;
- par divu konverģentu virkņu dalījumu.
- Pierādīt 3.16. teorēmas sekas.
- Pierādīt 3.17. teorēmu.
- Definēt funkcijas robežu punktā no kreisās puses.
- Pierādīt, ka divu bezgalīgi mazu funkciju summa un
reizinājums ir bezgalīgi maza funkcija.
- Pierādīt, ka bezgalīgi mazas funkcijas reizinājums ar
ierobežotu funkciju ir bezgalīgi maza funkcija.
- Pierādīt, ka bezgalīgi lielai funkcijai
 apgriezta
funkcija
apgriezta
funkcija
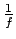 ir bezgalīgi maza funkcija.
ir bezgalīgi maza funkcija.
- Pierādīt, ka
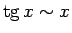
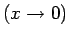 .
.
- Pierādīt, ka bezgalīgi lielas funkcijas modulis un
reizinājums ar konstanti
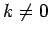 ir bezgalīgi lielas
funkcijas.
ir bezgalīgi lielas
funkcijas.
- Pierādīt, ka divu bezgalīgi lielu funkciju reizinājums
ir bezgalīgi liela funkcija.
- Pierādīt, ka bezgalīgi lielas funkcijas reizinājums ar
ierobežotu funkciju ir bezgalīgi liela funkcija.
- Pierādīt, ka bezgalīgi lielas funkcijas un ierobežotas
funkcijas summa ir bezgalīgi liela funkcija.
- Parādīt, ka
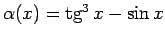 ir 3. kārtas
bezgalīgi maza funkcija, kad
ir 3. kārtas
bezgalīgi maza funkcija, kad
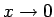 , salīdzinot ar
, salīdzinot ar
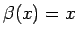 .
.
- Pierādīt 3.20. teorēmu.
- Pierādīt, ka dilstoša un ierobežota no apakšas virkne ir
konverģenta.
- Pierādīt, ka dilstošas un konverģentas virknes katrs
loceklis ir lielāks par šīs virknes robežu.
- Pierādīt, ka
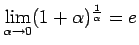 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4. FUNKCIJAS NEPĀRTRAUKTĪBA
Augstāk: 3.14. Skaitļu virknes konverģences Košī kritērijs
Iepriekšējais: 3.15. Jautājumi
2003-02-24

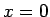 .
.
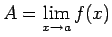 definīciju šādos gadījumos:
definīciju šādos gadījumos:
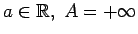 ;
;
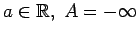 ;
;
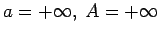 ;
;
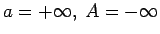 ;
;
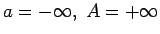 ;
;
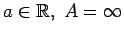 ;
;
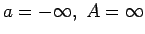 ;
;
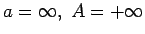 ;
;
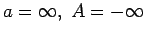 ;
;
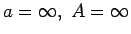 .
.
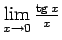 .
.
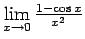 .
.
 apgriezta
funkcija
apgriezta
funkcija
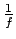 ir bezgalīgi maza funkcija.
ir bezgalīgi maza funkcija.
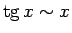
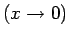 .
.
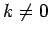 ir bezgalīgi lielas
funkcijas.
ir bezgalīgi lielas
funkcijas.
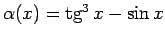 ir 3. kārtas
bezgalīgi maza funkcija, kad
ir 3. kārtas
bezgalīgi maza funkcija, kad
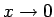 , salīdzinot ar
, salīdzinot ar
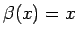 .
.
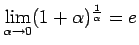 .
.