Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.4. Funkcijas pārtraukuma punkti un to
Augstāk: 4. FUNKCIJAS NEPĀRTRAUKTĪBA
Iepriekšējais: 4.2. Nepārtrauktu funkciju pamatīpašības
-
4.5. definīcija.
- Funkciju
 nosauksim par nepārtrauktu punktā
nosauksim par nepārtrauktu punktā
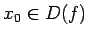 no kreisās puses (vai no labās puses), ja
no kreisās puses (vai no labās puses), ja
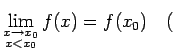
vai
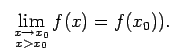
4.1. zīm. attēlota nepārtraukta punktā  no kreisās
puses funkcija, bet 4.2. zīmējumā - nepārtraukta punktā
no kreisās
puses funkcija, bet 4.2. zīmējumā - nepārtraukta punktā
 no labās puses funkcija.
no labās puses funkcija.
Apskatīsim dažus piemērus.
![$ f(x)=[x]$](img209.gif) .
.
Ja  - vesels skaitlis, tad
Tas nozīmē, ka funkcija nepārtraukta visos šādos punktos no
labās puses.
- vesels skaitlis, tad
Tas nozīmē, ka funkcija nepārtraukta visos šādos punktos no
labās puses.
Tā kā
tad funkcija nav nepārtraukta punktā  no kreisās puses.
Piemēram,
no kreisās puses.
Piemēram, 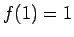 ,
,
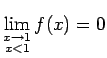 ,
,
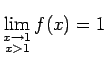 (2.5. zīm.).
(2.5. zīm.).
Pārējos punktos šī funkcija ir nepārtraukta gan no kreisās,
gan no labās puses.
-
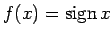 .
.
Šai funkcijai 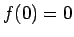 ,
,
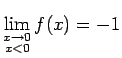 ,
,
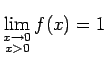 (3.27. zīm.). Tāpēc tā nav nepārtraukta punktā
(3.27. zīm.). Tāpēc tā nav nepārtraukta punktā
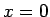 ne no kreisās, ne no labās puses.
ne no kreisās, ne no labās puses.
-
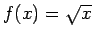 .
.
Funkcija nav definēta pa kreisi no punkta 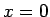 un
un
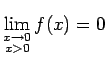 (4.3. zīm.).
(4.3. zīm.).
-
4.1. piez
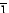 me.
me.
- Ja punktā
 funkcija ir nepārtraukta,
piemēram, no labās puses, bet pa kreisi no šī punkta tā nav
definēta, tad uzskatīsim, ka funkcija ir nepārtraukta punktā
funkcija ir nepārtraukta,
piemēram, no labās puses, bet pa kreisi no šī punkta tā nav
definēta, tad uzskatīsim, ka funkcija ir nepārtraukta punktā
 .
.
Tātad funkcija
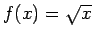 ir nepārtraukta punktā
ir nepārtraukta punktā 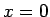 . Ar
funkcijas robežu tādā punktā saprot tās vienpusējo robežu. Šajā
piemērā
. Ar
funkcijas robežu tādā punktā saprot tās vienpusējo robežu. Šajā
piemērā
-
4.9. teorēma.
- Funkcija
 ir nepārtraukta
punktā 4.2
ir nepārtraukta
punktā 4.2  tad un tikai tad, ja tā ir nepārtraukta šajā
punktā gan no kreisās, gan no labās puses.
tad un tikai tad, ja tā ir nepārtraukta šajā
punktā gan no kreisās, gan no labās puses.
 Nepieciešamība. Tā kā
funkcija
Nepieciešamība. Tā kā
funkcija  nepārtraukta punktā
nepārtraukta punktā  , tad
, tad
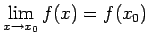 . Tas nozīmē, ka šajā
punktā funkcijai eksistē vienādas vienpusējās robežas
. Tas nozīmē, ka šajā
punktā funkcijai eksistē vienādas vienpusējās robežas
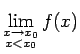 ,
,
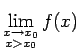 un šīs
robežas ir vienādas ar
un šīs
robežas ir vienādas ar 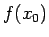 . Seko, ka funkcija nepārtraukta
punktā
. Seko, ka funkcija nepārtraukta
punktā  gan no kreisās, gan no labās puses.
gan no kreisās, gan no labās puses.
Pietiekamība. Tā kā funkcija  nepārtraukta
punktā
nepārtraukta
punktā  gan no kreisās, gan no labās puses, tad
gan no kreisās, gan no labās puses, tad
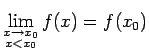
un
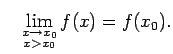
Seko, ka eksistē
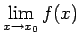 un tā ir vienāda ar
un tā ir vienāda ar 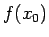 .
Funkcija
.
Funkcija  ir nepārtraukta punktā
ir nepārtraukta punktā  .
.
-
4.2. piez
 me.
me.
- Šī teorēma ļauj punktā
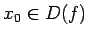 nepārtrauktu funkciju definēt ar šādu vienādību
nepārtrauktu funkciju definēt ar šādu vienādību
Piemēram, funkcijai
Tātad
t.i.,
funkcija ir nepārtraukta punktā 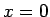 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.4. Funkcijas pārtraukuma punkti un to
Augstāk: 4. FUNKCIJAS NEPĀRTRAUKTĪBA
Iepriekšējais: 4.2. Nepārtrauktu funkciju pamatīpašības
2003-02-24
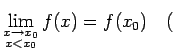 vai
vai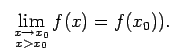
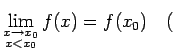 vai
vai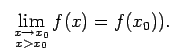
![]() no kreisās
puses funkcija, bet 4.2. zīmējumā - nepārtraukta punktā
no kreisās
puses funkcija, bet 4.2. zīmējumā - nepārtraukta punktā
![]() no labās puses funkcija.
no labās puses funkcija.
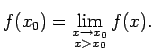
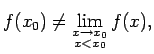
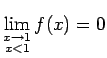 ,
,
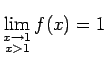 (2.5. zīm.).
(2.5. zīm.).
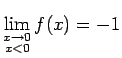 ,
,
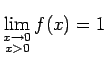 (3.27. zīm.). Tāpēc tā nav nepārtraukta punktā
(3.27. zīm.). Tāpēc tā nav nepārtraukta punktā
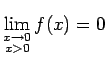 (4.3. zīm.).
(4.3. zīm.).
![]() ir nepārtraukta punktā
ir nepārtraukta punktā ![]() . Ar
funkcijas robežu tādā punktā saprot tās vienpusējo robežu. Šajā
piemērā
. Ar
funkcijas robežu tādā punktā saprot tās vienpusējo robežu. Šajā
piemērā
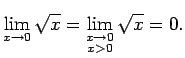
![]() Nepieciešamība. Tā kā
funkcija
Nepieciešamība. Tā kā
funkcija ![]() nepārtraukta punktā
nepārtraukta punktā ![]() , tad
, tad
![]() . Tas nozīmē, ka šajā
punktā funkcijai eksistē vienādas vienpusējās robežas
. Tas nozīmē, ka šajā
punktā funkcijai eksistē vienādas vienpusējās robežas
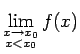 ,
,
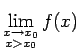 un šīs
robežas ir vienādas ar
un šīs
robežas ir vienādas ar ![]() . Seko, ka funkcija nepārtraukta
punktā
. Seko, ka funkcija nepārtraukta
punktā ![]() gan no kreisās, gan no labās puses.
gan no kreisās, gan no labās puses.
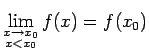 un
un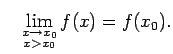
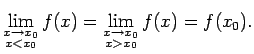
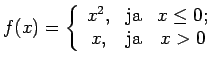
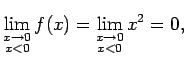
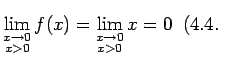 zīm
zīm