Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.3. Funkcijas vienpusējā nepārtrauktība
Augstāk: 4. FUNKCIJAS NEPĀRTRAUKTĪBA
Iepriekšējais: 4.1. Nepārtrauktas funkcijas jēdziens
Nepārtrauktu funkciju svarīgākās īpašības apraksta šādas teorēmas.
-
4.1. teorēma.
- Nepārtrauktas funkcijas modulis ir
nepārtraukta funkcija.
-
4.2. teorēma.
- Nepārtrauktas funkcijas
reizinājums ar konstanti ir nepārtraukta funkcija.
-
4.3. teorēma.
- Divu nepārtrauktu funkciju summa
ir nepārtraukta funkcija.
-
4.4. teorēma.
- Divu nepārtrauktu funkciju
reizinājums
ir nepārtraukta funkcija.
-
4.5. teorēma.
- Divu nepārtrauktu funkciju
dalījums
ir nepārtraukta funkcija.
Pierādīsim tikai vienu no šīm teorēmām, piemēram,
4.5. teorēmu.
 Izvēlēsimies patvaļīgu
Izvēlēsimies patvaļīgu
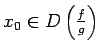 . Šis punkts
. Šis punkts
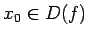 un
un
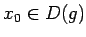 . Tā kā funkcijas
. Tā kā funkcijas  un
un 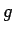 ir nepārtrauktas, tad
ir nepārtrauktas, tad
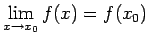
un
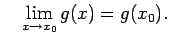
Saskaņā ar teorēmu
par divu funkciju dalījuma robežu eksistē
Tātad
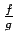 - nepārtraukta funkcija.
- nepārtraukta funkcija.
Līdzīgā veidā pierāda visas pārējās teorēmas.
-
4.6. teorēma.
- [Par robežpāreju zem nepārtrauktas funkcijas
zīmes]
Ja eksistē galīga robeža
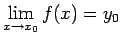 un funkcija
un funkcija 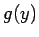 nepārtraukta punktā
nepārtraukta punktā 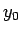 , tad
, tad
 Tā kā funkcija
Tā kā funkcija 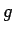 nepārtraukta punktā
nepārtraukta punktā
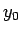 , tad
, tad
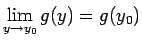 . Saskaņā ar saliktas funkcijas
. Saskaņā ar saliktas funkcijas
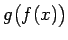 robežu
robežu
- Sekas.
- Ja funkcija
 nepārtraukta punktā
nepārtraukta punktā  un
virkne
un
virkne
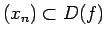 konverģē uz
konverģē uz  , tad
funkcijas vērtību virkne
, tad
funkcijas vērtību virkne
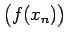 konverģē uz
konverģē uz
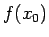 .
.
 Tā kā virkne
Tā kā virkne 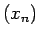 konverģē uz
konverģē uz  , tad
, tad
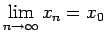 . Tā kā funkcija
. Tā kā funkcija  nepārtraukta punktā
nepārtraukta punktā  , tad
, tad
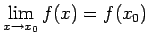 . Saskaņā ar 4.6. teorēmu
. Saskaņā ar 4.6. teorēmu
Seko, ka virkne
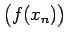 konverģē uz
konverģē uz 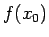 .
.
-
4.7. teorēma.
- Ja jebkurai uz
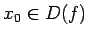 konverģentai virknei
konverģentai virknei
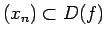 atbilstošā virkne
atbilstošā virkne
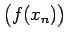 konverģē uz
konverģē uz 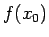 , tad funkcija
, tad funkcija  nepārtraukta punktā
nepārtraukta punktā  .
.
Šo teorēmu viegli pierādīt no pretējā.
No 4.6. teorēmas sekām un 4.7. teorēmas izriet
punktā nepārtrauktas funkcijas vēl viena definīcija
(līdzvērtīga iepriekšējām).
-
4.4. definīcija.
- (Pēc Heines4.1 jeb virkņu
valodā).
Funkciju  nosauksim par nepārtrauktu punktā
nosauksim par nepārtrauktu punktā
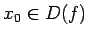 ,
ja jebkurai virknei
,
ja jebkurai virknei
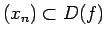 , kas konverģē uz
, kas konverģē uz
 , atbilstošā virkne
, atbilstošā virkne
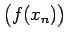 konverģē uz
konverģē uz
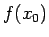 .
.
-
4.8. teorēma.
- (Par saliktas funkcijas nepārtrauktību)
Ja funkcija  nepārtraukta punktā
nepārtraukta punktā  un
un 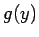 nepārtraukta atbilstošajā punktā
nepārtraukta atbilstošajā punktā 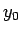 , kur
, kur
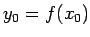 , tad
salikta funkcija
, tad
salikta funkcija
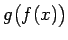 nepārtraukta punktā
nepārtraukta punktā
 .
.
Pierāda, izmantojot 3.15. teorēmu par saliktas funkcijas
robežu.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.3. Funkcijas vienpusējā nepārtrauktība
Augstāk: 4. FUNKCIJAS NEPĀRTRAUKTĪBA
Iepriekšējais: 4.1. Nepārtrauktas funkcijas jēdziens
2003-02-24
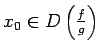 . Šis punkts
. Šis punkts
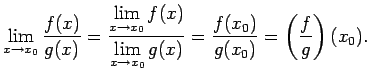
![]() Tā kā funkcija
Tā kā funkcija ![]() nepārtraukta punktā
nepārtraukta punktā
![]() , tad
, tad
![]() . Saskaņā ar saliktas funkcijas
. Saskaņā ar saliktas funkcijas
![]() robežu
robežu
![]() Tā kā virkne
Tā kā virkne ![]() konverģē uz
konverģē uz ![]() , tad
, tad
![]() . Tā kā funkcija
. Tā kā funkcija ![]() nepārtraukta punktā
nepārtraukta punktā ![]() , tad
, tad
![]() . Saskaņā ar 4.6. teorēmu
. Saskaņā ar 4.6. teorēmu