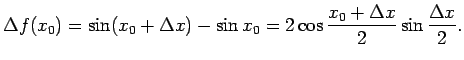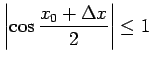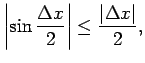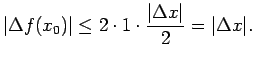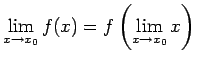 , citiem vārdiem,
, citiem vārdiem,
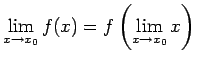 , citiem vārdiem,
, citiem vārdiem,
No funkcijas robežas definīcijas izriet, ka funkciju ![]() nosauksim
par nepārtrauktu punktā
nosauksim
par nepārtrauktu punktā
![]() , ja jebkuram
, ja jebkuram
![]() eksistē tāds
eksistē tāds ![]() , ka visiem
, ka visiem ![]() , kuriem
, kuriem
![]() , izpildīsies nevienādība
, izpildīsies nevienādība
Apzīmēsim ![]() ar
ar ![]() un nosauksim par argumenta
pieaugumu punktā
un nosauksim par argumenta
pieaugumu punktā ![]() , bet
, bet
![]() ar
ar
![]() un
nosauksim par funkcijas pieaugumu punktā
un
nosauksim par funkcijas pieaugumu punktā ![]() , kas
atbilst argumenta pieaugumam
, kas
atbilst argumenta pieaugumam ![]() . Šajos apzīmējumos punktā
nepārtrauktas funkcijas definīcija būs šāda: funkciju
. Šajos apzīmējumos punktā
nepārtrauktas funkcijas definīcija būs šāda: funkciju ![]() nosauksim par nepārtrauktu punktā
nosauksim par nepārtrauktu punktā
![]() , ja jebkuram
, ja jebkuram
![]() eksistē tāds
eksistē tāds ![]() , ka visiem
, ka visiem ![]() , kuriem
, kuriem
![]() , izpildīsies nevienādība
, izpildīsies nevienādība
![]() . Tas nozīmē, ka mazam argumenta pieaugumam
atbilst mazs funkcijas pieaugums, t.i.,
. Tas nozīmē, ka mazam argumenta pieaugumam
atbilst mazs funkcijas pieaugums, t.i.,
Turpmāk, lai pierādītu funkcijas nepārtrauktību, vajadzēs pierādīt
tās nepārtrauktību definīcijas apgabala patvaļīgajā punktā ![]() .
.
Apskatīsim dažu nepārtrauktu funkciju piemērus.
Visiem
Patvaļīgam
Patvaļīgam