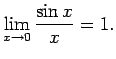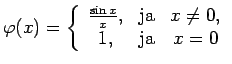Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.5. Monotonas funkcijas robeža un tās
Augstāk: 4. FUNKCIJAS NEPĀRTRAUKTĪBA
Iepriekšējais: 4.3. Funkcijas vienpusējā nepārtrauktība
-
4.6. definīcija.
- Punktu
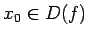 nosauksim par funkcijas
pārtraukuma punktu, ja šajā punktā funkcija nav nepārtraukta.
nosauksim par funkcijas
pārtraukuma punktu, ja šajā punktā funkcija nav nepārtraukta.
Tātad visi funkcijas definīcijas apgabala punkti sadalās funkcijas
pārtraukuma un nepārtrauktības punktos.
Piemēram, funkcijai
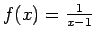 (4.5. zīm.)
definīcijas apgabals
(4.5. zīm.)
definīcijas apgabals
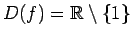 .
Pārtraukuma punktu šai funkcijai nav.
.
Pārtraukuma punktu šai funkcijai nav.
Funkcijai
(4.6. zīm.) definīcijas apgabala punkts 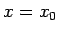 ir par
funkcijas pārtraukuma punktu, jo
ir par
funkcijas pārtraukuma punktu, jo 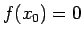 , bet
, bet
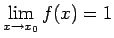 .
.
Funkcijai
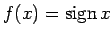 definīcijas apgabala punkts
definīcijas apgabala punkts 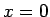 ir par
funkcijas pārtraukuma punktu, jo
ir par
funkcijas pārtraukuma punktu, jo
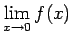 neeksistē (3.27. zīm.).
neeksistē (3.27. zīm.).
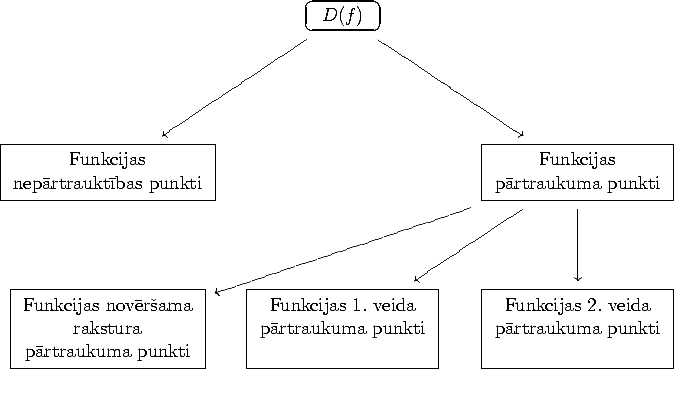
Funkcijas pārtraukuma punktu klasifikācija ir šāda: funkcijas
novēršama rakstura pārtraukuma punkti, funkcijas 1. veida
pārtraukuma punkti un funkcijas 2. veida pārtraukuma punkti.
4.7. zīm.
-
4.7. definīcija.
- Funkcijas pārtraukuma punktu
 nosauksim par
tās novēršama rakstura pārtraukuma punktu, ja punktā
nosauksim par
tās novēršama rakstura pārtraukuma punktu, ja punktā
 eksistē galīgas un vienādas funkcijas vienpusējās
robežas, bet tās nav vienādas ar funkcijas vērtību šajā
punktā, t.i.,
eksistē galīgas un vienādas funkcijas vienpusējās
robežas, bet tās nav vienādas ar funkcijas vērtību šajā
punktā, t.i.,
Tā kā punktā  funkcijas vienpusējās robežas sakrīt, tad šajā
punktā eksistē galīga robeža
funkcijas vienpusējās robežas sakrīt, tad šajā
punktā eksistē galīga robeža
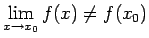 .
.
Piemēram, funkcijai
punkts 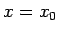 ir tās novēršama rakstura pārtraukuma punkts
(4.6. zīm.).
ir tās novēršama rakstura pārtraukuma punkts
(4.6. zīm.).
Apskatīsim funkciju
Funkcija 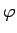 ir nepārtraukta punktā
ir nepārtraukta punktā  . Šādā veidā,
punktā
. Šādā veidā,
punktā  izmainot funkcijas vērtību, funkcijas pārtraukuma
punktu
izmainot funkcijas vērtību, funkcijas pārtraukuma
punktu  izdevās novērst.
izdevās novērst.
-
4.8. definīcija.
- Funkcijas pārtraukuma punktu
 nosauksim par
tās 1. veida pārtraukuma punktu, ja punktā
nosauksim par
tās 1. veida pārtraukuma punktu, ja punktā  eksistē galīgas un dažādas funkcijas vienpusējās robežas,
t.i.,
eksistē galīgas un dažādas funkcijas vienpusējās robežas,
t.i.,
Acīmredzot, šoreiz
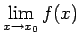 neeksistē.
neeksistē.
Piemēram, funkcijai
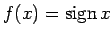 punkts
punkts 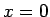 ir tās 1. veida
pārtraukuma punkts (3.27. zīm.).
ir tās 1. veida
pārtraukuma punkts (3.27. zīm.).
-
4.9. definīcija.
- Funkcijas pārtraukuma punktu
 , kas nav ne
funkcijas novēršama rakstura pārtraukuma punkts, ne funkcijas
1. veida pārtraukuma punkts, nosauksim par funkcijas 2. veida
pārtraukuma punktu.
, kas nav ne
funkcijas novēršama rakstura pārtraukuma punkts, ne funkcijas
1. veida pārtraukuma punkts, nosauksim par funkcijas 2. veida
pārtraukuma punktu.
Acīmredzami, funkcijas 2. veida pārtraukuma punkti ir tie
pārtraukuma punkti, kuros vismaz viena no šīs funkcijas
vienpusējām robežām ir bezgalība vai vispār neeksistē.
Piemēram, funkcijai
(4.8. zīm.) tās pārtraukuma punkts 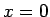 ir funkcijas
2. veida pārtraukuma punkts, jo
ir funkcijas
2. veida pārtraukuma punkts, jo
Apskatīsim vēl dažus iespējamus gadījumus:
- Funkcija definēta punktā
 un tikai, piemēram, pa
labi no punkts
un tikai, piemēram, pa
labi no punkts  .
.
- Eksistē galīga
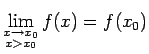 .
.
Kā tika atzīmēts iepriekš,
uzskatīsim, ka eksistē
un ka  nepārtraukta šajā punktā.
nepārtraukta šajā punktā.
- Eksistē galīga
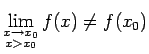 .
.
Arī šoreiz uzskatīsim, ka eksistē
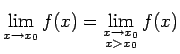 .
Punkts
.
Punkts  būs funkcijas novēršama rakstura pārtraukuma
punkts.
būs funkcijas novēršama rakstura pārtraukuma
punkts.
- Robeža
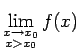 neeksistē vai ir bezgalība. Punkts
neeksistē vai ir bezgalība. Punkts  būs funkcijas 2. veida pārtraukuma punkts.
būs funkcijas 2. veida pārtraukuma punkts.
- Ja punkts
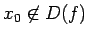 un eksistē galīga
un eksistē galīga
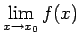 , tad funkciju var definēt punktā
, tad funkciju var definēt punktā  , turpinot to
pēc nepārtrauktības, t.i.,
, turpinot to
pēc nepārtrauktības, t.i.,
Piemēram, funkcija
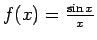 nav definēta punktā
nav definēta punktā
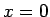 un eksistē
un eksistē
Funkcija
būs nepārtraukta punktā 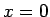 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.5. Monotonas funkcijas robeža un tās
Augstāk: 4. FUNKCIJAS NEPĀRTRAUKTĪBA
Iepriekšējais: 4.3. Funkcijas vienpusējā nepārtrauktība
2003-02-24
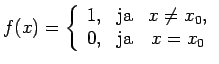
![]() definīcijas apgabala punkts
definīcijas apgabala punkts ![]() ir par
funkcijas pārtraukuma punktu, jo
ir par
funkcijas pārtraukuma punktu, jo
![]() neeksistē (3.27. zīm.).
neeksistē (3.27. zīm.).
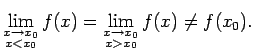
![]() funkcijas vienpusējās robežas sakrīt, tad šajā
punktā eksistē galīga robeža
funkcijas vienpusējās robežas sakrīt, tad šajā
punktā eksistē galīga robeža
![]() .
.
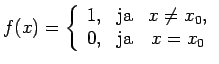
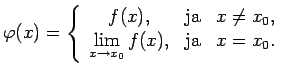
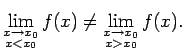
![]() neeksistē.
neeksistē.
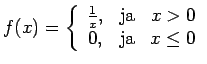
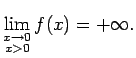
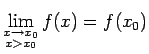 .
.
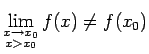 .
.
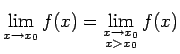 .
Punkts
.
Punkts 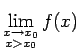 neeksistē vai ir bezgalība. Punkts
neeksistē vai ir bezgalība. Punkts 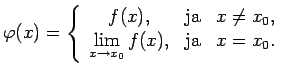
![]() nav definēta punktā
nav definēta punktā
![]() un eksistē
un eksistē