


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.6. Bolcano teorēma par nepārtrauktas funkcijas
Augstāk: 4. FUNKCIJAS NEPĀRTRAUKTĪBA
Iepriekšējais: 4.4. Funkcijas pārtraukuma punkti un to
-
4.10. teorēma.
- Ja funkcija
 definēta punktā
definēta punktā
 un tā apkārtnē, monotona šajā apkārtnē, tad punktā
un tā apkārtnē, monotona šajā apkārtnē, tad punktā  tai eksistē galīgas vienpusējās robežas, pie tam augošai vai
nedilstošai funkcijai
dilstošai vai neaugošai funkcijai
tai eksistē galīgas vienpusējās robežas, pie tam augošai vai
nedilstošai funkcijai
dilstošai vai neaugošai funkcijai
 Apskatīsim tikai augošu funkciju.
Apzīmēsim ar
Apskatīsim tikai augošu funkciju.
Apzīmēsim ar  kopu, kas sastāv no punkta
kopu, kas sastāv no punkta  minētās
apkārtnes tiem punktiem
minētās
apkārtnes tiem punktiem  , kuriem
, kuriem 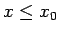 . Visiem
. Visiem 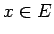 izpildīsies nevienādība
izpildīsies nevienādība
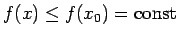 . Tas nozīmē, ka
kopā
. Tas nozīmē, ka
kopā  funkcija
funkcija  ierobežota no augšas ar
ierobežota no augšas ar 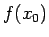 . Tātad kopā
. Tātad kopā
 eksistē galīgs funkcijas augšējais slieksnis4.3
eksistē galīgs funkcijas augšējais slieksnis4.3
pie tam
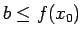 . Saskaņā ar kopas augšējā sliekšņa
definīciju eksistē tāds
. Saskaņā ar kopas augšējā sliekšņa
definīciju eksistē tāds 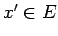 , ka
, ka
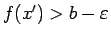 .
.
Tā kā funkcija  ir augoša, tad visiem
ir augoša, tad visiem  , kuriem
, kuriem 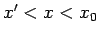 ,
izpildīsies nevienādība
,
izpildīsies nevienādība
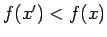 .
.
Ievērojot, ka
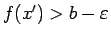 , iegūsim
, iegūsim
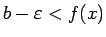 .
Acīmredzami,
.
Acīmredzami,
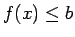 , tāpēc visiem šādiem
, tāpēc visiem šādiem 
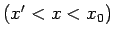 izpildīsies nevienādība
izpildīsies nevienādība
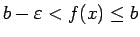
vai
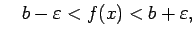
t.i.,
Tātad punktā  eksistē galīga robeža no kreisās puses un tā ir
vienāda ar
eksistē galīga robeža no kreisās puses un tā ir
vienāda ar 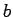 , t.i.,
, t.i.,
pie tam
jo
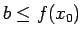 .
.
Ja apzīmē ar  kopu, kas sastāv no punkta
kopu, kas sastāv no punkta  minētās
apkārtnes tiem punktiem
minētās
apkārtnes tiem punktiem  , kuriem
, kuriem 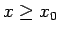 un rīkojas
līdzīgi, tad iegūst, ka punktā
un rīkojas
līdzīgi, tad iegūst, ka punktā  eksistē galīga robeža no
labās puses, pie tam
eksistē galīga robeža no
labās puses, pie tam
-
4.11. teorēma.
- Punktā
 un tā apkārtnē
definēta un monotona funkcija ir vai nu nepārtraukta šajā
punktā, vai
un tā apkārtnē
definēta un monotona funkcija ir vai nu nepārtraukta šajā
punktā, vai  ir šīs funkcijas 1. veida pārtraukuma
punkts.
ir šīs funkcijas 1. veida pārtraukuma
punkts.
 Apskatīsim tikai augošu funkciju.
Saskaņā ar iepriekšējo teorēmu punktā
Apskatīsim tikai augošu funkciju.
Saskaņā ar iepriekšējo teorēmu punktā  eksistē galīgas
vienpusējās robežas, pie tam
eksistē galīgas
vienpusējās robežas, pie tam
Iespējami šādi divi gadījumi:
-
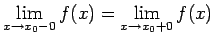 .
.
Acīmredzami, funkcija  ir nepārtraukta punktā
ir nepārtraukta punktā  , jo
eksistē
, jo
eksistē
-
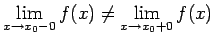 .
.
Šoreiz
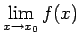 neeksistē. Punkts
neeksistē. Punkts
 ir funkcijas 1. veida pārtraukuma punkts.
ir funkcijas 1. veida pārtraukuma punkts.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.6. Bolcano teorēma par nepārtrauktas funkcijas
Augstāk: 4. FUNKCIJAS NEPĀRTRAUKTĪBA
Iepriekšējais: 4.4. Funkcijas pārtraukuma punkti un to
2003-02-24
![]() Apskatīsim tikai augošu funkciju.
Apzīmēsim ar
Apskatīsim tikai augošu funkciju.
Apzīmēsim ar ![]() kopu, kas sastāv no punkta
kopu, kas sastāv no punkta ![]() minētās
apkārtnes tiem punktiem
minētās
apkārtnes tiem punktiem ![]() , kuriem
, kuriem ![]() . Visiem
. Visiem ![]() izpildīsies nevienādība
izpildīsies nevienādība
![]() . Tas nozīmē, ka
kopā
. Tas nozīmē, ka
kopā ![]() funkcija
funkcija ![]() ierobežota no augšas ar
ierobežota no augšas ar ![]() . Tātad kopā
. Tātad kopā
![]() eksistē galīgs funkcijas augšējais slieksnis4.3
eksistē galīgs funkcijas augšējais slieksnis4.3
![]() eksistē galīga robeža no kreisās puses un tā ir
vienāda ar
eksistē galīga robeža no kreisās puses un tā ir
vienāda ar ![]() , t.i.,
, t.i.,
![]() Apskatīsim tikai augošu funkciju.
Saskaņā ar iepriekšējo teorēmu punktā
Apskatīsim tikai augošu funkciju.
Saskaņā ar iepriekšējo teorēmu punktā ![]() eksistē galīgas
vienpusējās robežas, pie tam
eksistē galīgas
vienpusējās robežas, pie tam