


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.7. Apvērstas funkcijas nepārtrauktība
Augstāk: 4. FUNKCIJAS NEPĀRTRAUKTĪBA
Iepriekšējais: 4.5. Monotonas funkcijas robeža un tās
-
4.12. teorēma.
- [Bolcano teorēma]
Ja funkcija  ir nepārtraukta
intervālā
ir nepārtraukta
intervālā
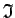 , tad patvaļīgiem
, tad patvaļīgiem
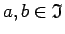 , kuriem
, kuriem
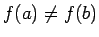 un patvaļīgam
un patvaļīgam
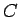 , kas atrodas starp
, kas atrodas starp 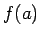 un
un 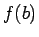 , eksistē tāds
, eksistē tāds 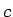 , kas
atrodas starp
, kas
atrodas starp  un
un 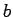 , ka
, ka 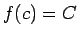 .
.
 Pieņemsim, ka
Pieņemsim, ka 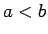 . Apzīmēsim ar
. Apzīmēsim ar
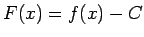 . Funkcija
. Funkcija 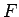 arī nepārtraukta intervālā
arī nepārtraukta intervālā
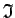 , pie tam tai vērtības slēgtā intervāla
, pie tam tai vērtības slēgtā intervāla ![$ [a;b]$](img958.gif) galapunktos ir ar pretējām zīmēm, jo
galapunktos ir ar pretējām zīmēm, jo
(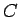 atrodas starp
atrodas starp 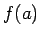 un
un 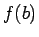 ).
).
Parādīsim, ka intervālā ![$ [a;b]$](img958.gif) eksistē tāds punkts
eksistē tāds punkts 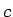 , kurā
, kurā
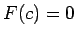 , t.i.,
, t.i., 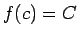 .
.
Intervālu ![$ [a;b]$](img958.gif) sadalīsim uz pusēm. Ja dalījuma punktā funkcijas
sadalīsim uz pusēm. Ja dalījuma punktā funkcijas
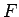 vērtība ir nulle, tad teorēma ir pierādīta. Pretējā gadījumā
to daļu, kuras galapunktos funkcijas
vērtība ir nulle, tad teorēma ir pierādīta. Pretējā gadījumā
to daļu, kuras galapunktos funkcijas 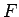 vērtības ir ar pretējām
zīmēm, apzīmēsim ar
vērtības ir ar pretējām
zīmēm, apzīmēsim ar ![$ [a_1;b_1]$](img961.gif) . Ar intervālu
. Ar intervālu ![$ [a_1;b_1]$](img961.gif) rīkosimies tāpat kā ar
rīkosimies tāpat kā ar ![$ [a;b]$](img958.gif) .
.
Ja kādā no dalīšanas etapiem nonāksim pie tāda dalījuma punkta,
kurā funkcijas 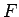 vērtība ir nulle, tad dalīšanas procesu
pārtrauc un teorēma ir pierādīta. Ja dalīšanas process turpinās
bezgalīgi, tad iegūsim savelkošos slēgtu intervālu virkni
kurai eksistē vienīgais kopīgais punkts
vērtība ir nulle, tad dalīšanas procesu
pārtrauc un teorēma ir pierādīta. Ja dalīšanas process turpinās
bezgalīgi, tad iegūsim savelkošos slēgtu intervālu virkni
kurai eksistē vienīgais kopīgais punkts 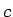 . Šis punkts
. Šis punkts 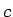 pieder
visiem intervāliem, tai skaitā, arī intervālam
pieder
visiem intervāliem, tai skaitā, arī intervālam ![$ [a;b]$](img958.gif) .
Saskaņā ar dalīšanas procesa nosacījumu
Pāriesim pie robežas, kad
.
Saskaņā ar dalīšanas procesa nosacījumu
Pāriesim pie robežas, kad  tiecas uz bezgalību un iegūsim
jeb
tiecas uz bezgalību un iegūsim
jeb
Tā kā
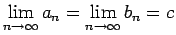 ,
tad iegūsim, ka
,
tad iegūsim, ka
Seko, ka 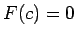 jeb
jeb 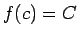 . Punkts
. Punkts 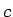 nesakrīt ne ar punktu
nesakrīt ne ar punktu
 , ne ar punktu
, ne ar punktu 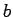 , jo
, jo 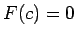 , bet
, bet
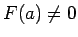 un
un
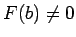 (4.9. zīm.).
(4.9. zīm.).
Šādi punkti 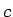 , kuros
, kuros 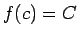 , var būt arī vairāki. Stingri
monotonai funkcijai tāds punkts
, var būt arī vairāki. Stingri
monotonai funkcijai tāds punkts 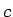 ir vienīgs.
ir vienīgs.
No šīs teorēmas izriet, ka nepārtrauta funkcija intervālu attēlo
par intervālu.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.7. Apvērstas funkcijas nepārtrauktība
Augstāk: 4. FUNKCIJAS NEPĀRTRAUKTĪBA
Iepriekšējais: 4.5. Monotonas funkcijas robeža un tās
2003-02-24
![]() Pieņemsim, ka
Pieņemsim, ka ![]() . Apzīmēsim ar
. Apzīmēsim ar
![]() . Funkcija
. Funkcija ![]() arī nepārtraukta intervālā
arī nepārtraukta intervālā
![]() , pie tam tai vērtības slēgtā intervāla
, pie tam tai vērtības slēgtā intervāla ![]() galapunktos ir ar pretējām zīmēm, jo
galapunktos ir ar pretējām zīmēm, jo
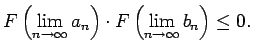
![]() ,
tad iegūsim, ka
,
tad iegūsim, ka
![]() , kuros
, kuros ![]() , var būt arī vairāki. Stingri
monotonai funkcijai tāds punkts
, var būt arī vairāki. Stingri
monotonai funkcijai tāds punkts ![]() ir vienīgs.
ir vienīgs.