


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.8. Slēgtā intervālā nepārtrauktu funkciju pamatīpašības
Augstāk: 4. FUNKCIJAS NEPĀRTRAUKTĪBA
Iepriekšējais: 4.6. Bolcano teorēma par nepārtrauktas funkcijas
-
4.13. teorēma.
- Ja funkcija
 nepārtraukta un
stingri monotona
intervālā
nepārtraukta un
stingri monotona
intervālā
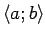 , tad tās apvērstā funkcija
, tad tās apvērstā funkcija 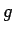 nepārtraukta atbilstošajā intervālā.
nepārtraukta atbilstošajā intervālā.
 Funkcijai
Funkcijai  apvērsta funkcija
apvērsta funkcija 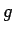 eksistē,
jo
eksistē,
jo  stingri monotona funkcija. Apzīmēsim ar
stingri monotona funkcija. Apzīmēsim ar
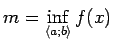 un
un
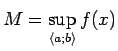 . Tā kā
. Tā kā  nepārtraukta funkcija, tad tā attēlo intervālu
nepārtraukta funkcija, tad tā attēlo intervālu
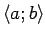 par intervālu
par intervālu
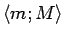 , kurā ir definēta
tās apvērstā funkcija
, kurā ir definēta
tās apvērstā funkcija 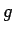 .
.
Apskatīsim tikai gadījumu, kad  augoša funkcija. Tās apvērstā
funkcija
augoša funkcija. Tās apvērstā
funkcija 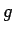 arī būs augoša funkcija.
arī būs augoša funkcija.
Izvēlēsimies patvaļīgu 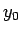
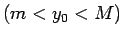 un parādīsim, ka funkcija
un parādīsim, ka funkcija
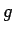 nepārtraukta punktā
nepārtraukta punktā 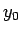 . Saskaņā ar Bolcano teorēmu (skat.
4.12. teorēmu) par nepārtrauktas funkcijas starpvērtībām
eksistē
tāds
. Saskaņā ar Bolcano teorēmu (skat.
4.12. teorēmu) par nepārtrauktas funkcijas starpvērtībām
eksistē
tāds
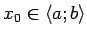 , ka
, ka
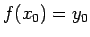 jeb
jeb
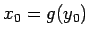 .
.
Izvēlēsimies jebkuru
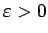 , bet tādu, lai
Tā kā
, bet tādu, lai
Tā kā  nepārtraukta un augoša funkcija, tad tā attēlo šo slēgto
intervālu par intervālu
nepārtraukta un augoša funkcija, tad tā attēlo šo slēgto
intervālu par intervālu
![$ \bigl[f(x_0-\varepsilon);
f(x_0+\varepsilon)\bigr]$](img979.gif) . Tā kā
tad
. Tā kā
tad
Izvēlēsimies punkta 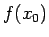 tādu
tādu 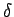 -apkārtni, lai
-apkārtni, lai
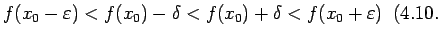
zīm.
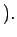
Jebkuram 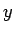 , kas piederēs punkta
, kas piederēs punkta
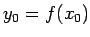
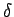 -apkārtnei, izpildīsies nevienādība
-apkārtnei, izpildīsies nevienādība
Tā kā 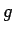 augoša funkcija, tad izpildīsies šāda nevienādība:
augoša funkcija, tad izpildīsies šāda nevienādība:
jeb
t.i., 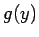 pieder punkta
pieder punkta 
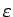 -apkārtnei.
-apkārtnei.
Seko, ka
t.i., funkcija 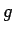 nepārtraukta punktā
nepārtraukta punktā 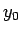 . Tā kā
. Tā kā 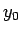 ir
patvaļīgs punkts, tad
ir
patvaļīgs punkts, tad 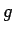 -nepārtraukta funkcija intervālā
-nepārtraukta funkcija intervālā
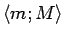 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.8. Slēgtā intervālā nepārtrauktu funkciju pamatīpašības
Augstāk: 4. FUNKCIJAS NEPĀRTRAUKTĪBA
Iepriekšējais: 4.6. Bolcano teorēma par nepārtrauktas funkcijas
2003-02-24
![]() Funkcijai
Funkcijai ![]() apvērsta funkcija
apvērsta funkcija ![]() eksistē,
jo
eksistē,
jo ![]() stingri monotona funkcija. Apzīmēsim ar
stingri monotona funkcija. Apzīmēsim ar
![]() un
un
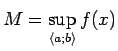 . Tā kā
. Tā kā ![]() nepārtraukta funkcija, tad tā attēlo intervālu
nepārtraukta funkcija, tad tā attēlo intervālu
![]() par intervālu
par intervālu
![]() , kurā ir definēta
tās apvērstā funkcija
, kurā ir definēta
tās apvērstā funkcija ![]() .
.
![]() tādu
tādu ![]() -apkārtni, lai
-apkārtni, lai
![]() , kas piederēs punkta
, kas piederēs punkta
![]()
![]() -apkārtnei, izpildīsies nevienādība
-apkārtnei, izpildīsies nevienādība
![]() augoša funkcija, tad izpildīsies šāda nevienādība:
augoša funkcija, tad izpildīsies šāda nevienādība: