Matemātika DU TSC
Nākamais: 4.9. Jautājumi Augstāk: 4. FUNKCIJAS NEPĀRTRAUKTĪBA Iepriekšējais: 4.7. Apvērstas funkcijas nepārtrauktība

4.8. Slēgtā intervālā nepārtrauktu funkciju
pamatīpašības

Slēgtā intervālā nepārtrauktu funkciju svarīgākās īpašības apraksta šādas trīs teorēmas: Veierštrāsa I teorēma, Veierštrāsa II teorēma un Kantora^4.4 teorēma.

4.14. teorēma. 

(Veierštrāsa I teorēma).

Slēgtā intervālā nepārtraukta funkcija ir ierobežota šajā intervālā.

$\blacktriangleright$ Pieņemsim pretējo, t.i., ka slēgtajā intervālā $[a;b]$ nepārtraukta funkcija $f$ nav ierobežota šajā intervālā. Intervālu $[a;b]$ sadalīsim trīs vienādās daļās un to intervālu, kurā funkcija nav ierobežota, apzīmēsim ar $[a_1;b_1]$. (Tāds intervāls, acīmredzami, eksistē). Ar intervālu $[a_1;b_1]$ rīkosimies tāpat kā ar $[a;b]$. Turpinot šo procesu bezgalīgi, iegūsim savelkošos slēgtu intervālu virkni

$$[a;b]\supset[a_1;b_1]\supset\cdots\supset[a_n;b_n]\supset\cdots\/,$$

kur

$$b_n-a_n=\frac{b-a}{3^n}\xrightarrow[n\rightarrow\infty]{\;}0\/.$$

Saskaņā ar savelkošos slēgtu intervālu principu eksistē vienīgs visiem intervāliem kopīgais punkts $c$. Izvēlēsimies punkta $c\in[a;b]$ patvaļīgu $\delta$ -apkārtni $U(c;\delta)$. Kāds arī nebūtu $\delta>0$, eksistē tāds numurs $k$, ka intervāls $[a_k;b_k]\subset U(c;\delta)$. Saskaņā ar konstrukciju $f$ neierobežota intervālā $[a_k;b_k]$, tātad neierobežota arī apkārtnē $U(c;\delta)$. Tā kā $f$ nepārtraukta intervālā $[a;b]$, tad tā būs nepārtraukta arī punktā $c$. Saskaņā ar punktā nepārtrauktu funkciju īpašībām $f$ ierobežota punkta $c$ apkārtnē. Pretruna.  $\blacktriangleleft$

Vaļējā intervālā teorēma nav spēkā. Piemēram, intervālā $(0;1)$ nepārtraukta funkcija $f(x)=\frac{1}{x}$ nav ierobežota šajā intervālā.

Tikpat būtiska ir otra prasība - funkcijas nepārtrauktības nosacījums. Piemēram, funkcija

$$f(x)=\left\{\begin{array}{ccl} \frac{1}{x}, & \text{ja} & 0<x\leq 1, \\ 0, & \text{ja} & x=0 \\ \end{array}\right.$$

ir definēta slēgtā intervālā, bet nav ierobežota šajā intervālā.

4.15. teorēma. 

(Veierštrāsa II teorēma).

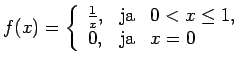
Slēgtā intervālā nepārtraukta funkcija sasniedz šajā intervālā savu vismazāko un vislielāko vērtību.

$\blacktriangleright$ Saskaņā ar iepriekšējo teorēmu funkcija $f$ ierobežota slēgtā intervālā $[a;b]$, t.i., eksistē galīgi $m=\inf\limits_{[a;b]}f(x)$ un $M=\sup\limits_{[a;b]}f(x)$.

Atliek tikai pierādīt, ka eksistē tādi punkti $c$, $C\in[a;b]$, ka $f(c)=m$ un $f(C)=M$. Pieņemsim pretējo, t.i., ka, piemēram, tāda $C\in[a;b]$, kurā funkcijas vērtība būtu vienāda ar $M$, nav. Tādā gadījumā visiem $x\in[a;b]$ $M-f(x)>0$ un funkcija $\frac{1}{M-f(x)}$ būs nepārtraukta šajā intervālā. Saskaņā ar iepriekšējo teorēmu šī funkcija būs ierobežota minētajā intervālā, t.i., eksistē tāds $p>0$, ka visiem $x\in[a;b]$, izpildīsies nevienādība

$$0<\frac{1}{M-f(x)}<p\/,$$

jeb

$$f(x)<M-\frac{1}{p}\/.$$

Šī nevienādība ir pretrunā ar funkcijas $f$ augšējā sliekšņa $M$ definīciju, jo saskaņā ar šo definīciju eksistē tāds $x'\in[a;b]$, ka

$$f(x')>M-\frac{1}{p}\quad\left(\frac{1}{p}>0\right)\/.$$

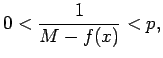
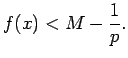
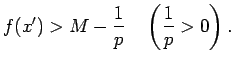
Līdzīgi var pierādīt, ka intervālā $[a;b]$ eksistē tāds punkts $c$, ka $f(c)=m$. $\blacktriangleleft$

Šādi punkti $c$ un $C$ var būt arī vairāki.

Funkcijas nepārtrauktības nosacījums ir būtisks, piemēram, funkcija

$$f(x)=\left\{\begin{array}{ccl} x+1, & \text{ja} & -1\leq x<0, \\ 0, & \text{ja} & x=0, \\ x-1,, & \text{ja} & 0<x\leq 1 \\ \end{array}\right.$$

(4.11. zīm.) intervālā $[0;1]$ nesasniedz ne savu vismazāko, ne savu vislielāko vērtību.

4.10. zīm.

4.10. definīcija. 

Funkciju $f$ nosauksim par vienmērīgi nepārtrauktu intervālā $\mathfrak{I}$, ja jebkuram $\varepsilon>0$ eksistē tāds $\delta>0$, ka visiem $x',x''\in\mathfrak{I}$, kuriem $\vert x''-x'\vert<\delta$, izpildās nevienādība

$$\vert f(x'')-f(x')\vert<\varepsilon\/.$$

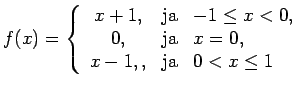
Acīmredzami, katra vienmērīgi nepārtraukta funkcija ir nepārtraukta funkcija. Apgriezts apgalvojums, vispārīgi runājot, nav spēkā.

Piemēram, $f(x)=\frac{1}{x}$ nepārtraukta intervālā $(0;1)$.

Apskatīsim izteiksmi

$$\vert f(x_2)-f(x_1)\vert=\frac{\vert x_2-x_1\vert}{x_1x_2}\/.$$

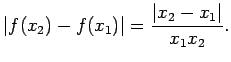
Izvēlēsimies $\varepsilon<1$, $x_1=\frac{\varepsilon}{n}$ un $x_2=\frac{\varepsilon}{n+1}$. Šādām argumenta vērtībām

$$\vert f(x_2)-f(x_1)\vert=\frac{1}{\varepsilon}>1\/.$$

Tātad, lai cik tuvas arī nebūtu argumenta vērtības $x_1$ un $x_2$, attālums starp to attēliem $f(x_1)$ un $f(x_2)$ ir lielāks par vienu.

4.16. teorēma. 

[Kantora teorēma]

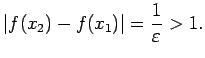
Slēgtā intervālā nepārtraukta funkcija ir vienmērīgi nepārtraukta šajā intervālā.

$\blacktriangleright$ Pieņemsim pretējo, t.i., ka funkcija $f$ nav vienmērīgi nepārtraukta intervālā $[a;b]$. Tas nozīmē, ka eksistē tāds $\varepsilon>0$, ka jebkuram $\delta>0$ varēs sameklēt $x'$ un $x''\in[a;b]$, kuriem $\vert x''-x'\vert<\delta$, bet izpildīsies nevienādība

$$\vert f(x'')-f(x')\vert\geq\varepsilon\/.$$

Izvēlēsimies pozitīvu skaitļu $\delta_n$ virkni $(\delta_n)$, kas konverģē uz nulli. Katram tādam $\delta_n$ varēs sameklēt $x_n'$ un $x''_n\in[a;b]$, kuriem $\vert x''_n-x'_n\vert<\delta_n$, bet izpildīsies nevienādība

$$\vert f(x''_n)-f(x'_n)\vert\geq\varepsilon\/.$$

Apskatīsim virkni $(x'_n)\subset[a;b]$, tātad šī virkne ir ierobežota. No šīs virknes var izdalīt konverģentu uz punktu $x_0\in[a;b]$ apakšvirkni $\left(x'_{n_k}\right)$. Šai virknei $\left(x'_{n_k}\right)$ atbilstoša virkne $\left(x''_{n_k}\right)$ konverģēs arī uz $x_0$, jo

$$\left\vert x''_{n_k}-x'_{n_k}\right\vert<\delta_{n_k}\xrightarrow[k\rightarrow\infty]{\;}0\/.$$

Tā kā funkcija $f$ nepārtraukta intervālā $[a;b]$, tad tā būs nepārtraukta punktā $x_0$.

Virknes $\left(f\bigl(x'_{n_k}\bigr)\right)$, $\left(f\bigl(x''_{n_k}\bigr)\right)$ konverģē uz $f(x_0)$, tātad

$$\left\vert f\left(x''_{n_k}\right)-f\left(x'_{n_k}\right)\right\vert\xrightarrow[k\rightarrow\infty]{\;}0\/,$$

kas pretrunā ar pieņēmumu, ka

$$\left\vert f\left(x''_{n_k}\right)-f\left(x'_{n_k}\right)\right\vert\geq\varepsilon\/.\;\blacktriangleleft$$

Matemātika DU TSC
Nākamais: 4.9. Jautājumi Augstāk: 4. FUNKCIJAS NEPĀRTRAUKTĪBA Iepriekšējais: 4.7. Apvērstas funkcijas nepārtrauktība