


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.6. Jautājumi
Augstāk: 1. REĀLO SKAITĻU KOPA
Iepriekšējais: 1.4. Intervāli kopā
-
1.7. definīcija.
- Par skaitļa
 (
(
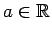 )
)
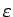 - apkārtni (
- apkārtni (
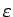 - pozitīvs
skaitlis) nosauksim vaļēju intervālu (
- pozitīvs
skaitlis) nosauksim vaļēju intervālu (
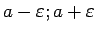 ) un apzīmēsim
) un apzīmēsim
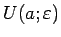 . Skaitli
. Skaitli
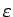 nosauksim par apkārtnes rādiusu.
nosauksim par apkārtnes rādiusu.
Seko, ka
-
1.8. definīcija.
- Par simbola
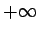
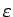 - apkārtni
nosauksim bezgalīgu intervālu (
- apkārtni
nosauksim bezgalīgu intervālu (
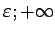 ) un
apzīmēsim
) un
apzīmēsim
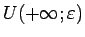 .
.
Analoģiski var definēt simbola 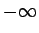
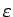 -
apkārtni
-
apkārtni
Acīmredzami, ja
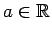 , tad
, tad
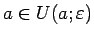 .
.
-
1.9. definīcija.
- Punktus
 un
un 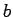 nosauksim par atdalāmiem ar
apkārtnēm, ja eksistē1.18 tādas šo punktu apkārtnes, kas nešķeļas.
nosauksim par atdalāmiem ar
apkārtnēm, ja eksistē1.18 tādas šo punktu apkārtnes, kas nešķeļas.
Apkārtņu īpašības:
- Divu (tātad jebkura galīga skaita) punkta
 apkārtņu
šķēlums ir šī punkta apkārtne.
apkārtņu
šķēlums ir šī punkta apkārtne.
- Jebkuri divi dažādi
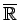 punkti
punkti  un
un 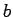 ir
atdalāmi ar apkārtnēm (pamatot patstāvīgi).
ir
atdalāmi ar apkārtnēm (pamatot patstāvīgi).



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.6. Jautājumi
Augstāk: 1. REĀLO SKAITĻU KOPA
Iepriekšējais: 1.4. Intervāli kopā
2003-02-24
![]()
![]() -
apkārtni
-
apkārtni
![]() , tad
, tad
![]() .
.