


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.5. Apkārtnes kopā
Augstāk: 1. REĀLO SKAITĻU KOPA
Iepriekšējais: 1.3. Reālo skaitļu kopas R ierobežotas kopas
Vēlāk, runājot par funkcijas robežu, būs izdevīgi papildināt reālo
skaitļu kopu
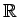 ar diviem simboliem
ar diviem simboliem 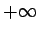 (plus
bezgalība) un
(plus
bezgalība) un 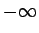 (mīnus bezgalība), sasaistot tos ar
reāliem skaitļiem ar šādām nevienādībām:
(mīnus bezgalība), sasaistot tos ar
reāliem skaitļiem ar šādām nevienādībām: 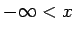 un
un
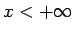 un savā starpā:
un savā starpā:
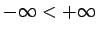 .
.
-
1.6. definīcija.
- Kopu
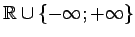 ar tajā
definētajām kārtības sakarībām un algebriskām darbībām, kas
definētas reālo skaitļu kopā
ar tajā
definētajām kārtības sakarībām un algebriskām darbībām, kas
definētas reālo skaitļu kopā
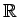 , nosauksim par
paplašināto reālo skaitļu kopu (paplašināto skaitļu taisni) un
apzīmēsim
, nosauksim par
paplašināto reālo skaitļu kopu (paplašināto skaitļu taisni) un
apzīmēsim
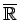 (skat. 1.16).
(skat. 1.16).
Acīmredzami,
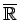 ir lineāri sakārtota kopa,
t.i., visiem
ir lineāri sakārtota kopa,
t.i., visiem
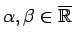 izpildās viena
un tikai viena no sakarībām
izpildās viena
un tikai viena no sakarībām
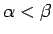 ,
,
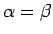 ,
,
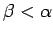 .
.
Matemātiskajā analīzē apskata ne tikai visu naturālo skaitļu kopu
 , bet arī tādas skaitliskas kopas kā intervālus, t.i.,
šādas kopas:
, bet arī tādas skaitliskas kopas kā intervālus, t.i.,
šādas kopas:
| |
![$\displaystyle [\alpha;\beta]=\{x\in\mathbb{R}\vert\alpha\leq x\leq\beta\}\;$](img115.gif) - slēgts intervāls; - slēgts intervāls; |
|
| |
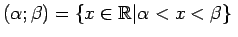 - vaļējs intervāls; - vaļējs intervāls; |
|
| |
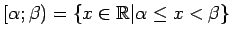 - pusvaļējs intervāls; - pusvaļējs intervāls; |
|
| |
![$\displaystyle (\alpha;\beta]=\{x\in\mathbb{R}\vert\alpha<x\leq\beta\}\;$](img118.gif) - pusvaļējs intervāls; - pusvaļējs intervāls; |
|
| |
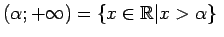 - bezgalīgs intervāls (skaitļu taisnes stars); - bezgalīgs intervāls (skaitļu taisnes stars); |
|
| |
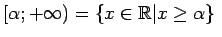 - bezgalīgs intervāls (skaitļu taisnes stari); - bezgalīgs intervāls (skaitļu taisnes stari); |
|
| |
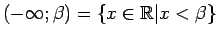 - bezgalīgs intervāls (skaitļu taisnes stars); - bezgalīgs intervāls (skaitļu taisnes stars); |
|
| |
![$\displaystyle (-\infty;\beta]=\{x\in\mathbb{R}\vert x\leq\beta\}\;$](img122.gif) - bezgalīgs intervāls (skaitļu taisnes stars); - bezgalīgs intervāls (skaitļu taisnes stars); |
|
| |
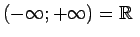 - visu reālo skaitļu kopa (skaitļu taisne). - visu reālo skaitļu kopa (skaitļu taisne). |
|
Visur
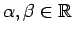 ;
;
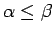 .
.
Vispārīgi visus šos intervālus apzīmēsim
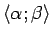 1.17.
Skaitļus, kas atrodas starp
1.17.
Skaitļus, kas atrodas starp 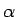 un
un 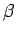 , nosauksim par
intervāla
, nosauksim par
intervāla
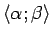 iekšējiem punktiem, bet
iekšējiem punktiem, bet
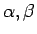 - par tā galapunktiem. Ja
- par tā galapunktiem. Ja
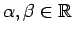 , tad
, tad
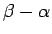 nosauksim par
intervāla
nosauksim par
intervāla
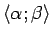 garumu.
garumu.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.5. Apkārtnes kopā
Augstāk: 1. REĀLO SKAITĻU KOPA
Iepriekšējais: 1.3. Reālo skaitļu kopas R ierobežotas kopas
2003-02-24
![]() ar diviem simboliem
ar diviem simboliem ![]() (plus
bezgalība) un
(plus
bezgalība) un ![]() (mīnus bezgalība), sasaistot tos ar
reāliem skaitļiem ar šādām nevienādībām:
(mīnus bezgalība), sasaistot tos ar
reāliem skaitļiem ar šādām nevienādībām: ![]() un
un
![]() un savā starpā:
un savā starpā:
![]() .
.
![]() ir lineāri sakārtota kopa,
t.i., visiem
ir lineāri sakārtota kopa,
t.i., visiem
![]() izpildās viena
un tikai viena no sakarībām
izpildās viena
un tikai viena no sakarībām
![]() ,
,
![]() ,
,
![]() .
.