


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.4. Intervāli kopā
Augstāk: 1. REĀLO SKAITĻU KOPA
Iepriekšējais: 1.2. Reālā skaitļa modulis
-
1.2. definīcija.
- Skaitli
 nosauksim par kopas
nosauksim par kopas
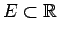 apakšējo robežu, ja visiem
apakšējo robežu, ja visiem
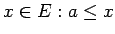 .
.
-
1.1. piez
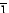 me.
me.
- Ja eksistē tāds
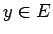 , kuram
, kuram 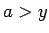 , tad
, tad  nav kopas
nav kopas  apakšējā robeža.
apakšējā robeža.
-
1.3. definīcija.
- Kopu
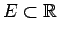 nosauksim par
ierobežotu no apakšas, ja tai eksistē apakšējā robeža.
(Pretējā gadījumā kopu nosauksim par neierobežotu no
apakšas).
nosauksim par
ierobežotu no apakšas, ja tai eksistē apakšējā robeža.
(Pretējā gadījumā kopu nosauksim par neierobežotu no
apakšas).
-
1.2. piez
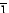 me.
me.
- Analoģiski var definēt kopas augšējo robežu un
ierobežotu no augšas kopu.
Piemēram, visu naturālo1.12 skaitļu kopa
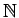 ir ierobežota no
apakšas, bet nav ierobežota no augšas. Visu veselo skaitļu kopa
ir ierobežota no
apakšas, bet nav ierobežota no augšas. Visu veselo skaitļu kopa
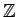 nav ierobežota ne no augšas, ne no apakšas.
nav ierobežota ne no augšas, ne no apakšas.
-
1.3. piez
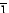 me.
me.
- Tukšo kopu uzskatīsim par ierobežotu gan no
augšas, gan no apakšas.
-
1.4. definīcija.
- Kopu
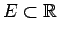 nosauksim par
ierobežotu, ja tā ir ierobežota gan no augšas, gan no apakšas.
nosauksim par
ierobežotu, ja tā ir ierobežota gan no augšas, gan no apakšas.
Piemēram, tukšā kopa ir ierobežota, bet visu veselo skaitļu kopa
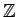 , visu naturālo skaitļu kopa
, visu naturālo skaitļu kopa
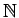 nav
ierobežotas kopas.
nav
ierobežotas kopas.
Viegli pamatot, ka kopa  ir ierobežota tad un tikai tad, kad ir
ierobežota no augšas kopa, kas sastādīta no tās elementu
moduļiem. (Pamatot to).
ir ierobežota tad un tikai tad, kad ir
ierobežota no augšas kopa, kas sastādīta no tās elementu
moduļiem. (Pamatot to).
-
1.5. definīcija.
- Par kopas
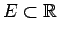 apakšējo
slieksni nosauksim vislielāko starp šīs kopas apakšējām
robežām un apzīmēsim
apakšējo
slieksni nosauksim vislielāko starp šīs kopas apakšējām
robežām un apzīmēsim
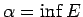 (lasa infīms1.13).
(lasa infīms1.13).
Analoģiski var definēt kopas augšējo slieksni
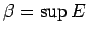 kā
kopas
kā
kopas  vismazāko augšējo robežu (lasa suprems1.14).
vismazāko augšējo robežu (lasa suprems1.14).
-
1.1. teorēma.
- 1.15 [Par ierobežotas kopas augšējā sliekšņa eksistenci]
Katrai netukšai un ierobežotai no augšas kopai
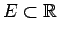 eksistē augšējais slieksnis.
eksistē augšējais slieksnis.
 Tā kā kopa
Tā kā kopa  ir ierobežota no augšas, tad
tai eksistē augšējā robeža. Apzīmēsim ar
ir ierobežota no augšas, tad
tai eksistē augšējā robeža. Apzīmēsim ar 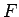 kopas
kopas  visu
augšējo robežu kopu. Acīmredzot,
visu
augšējo robežu kopu. Acīmredzot,
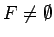 un
un 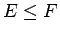 .
Saskaņā ar
.
Saskaņā ar
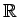 nepārtrauktības Dedekinda
aksiomu
eksistē tāds skaitlis
nepārtrauktības Dedekinda
aksiomu
eksistē tāds skaitlis 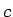 , ka
, ka
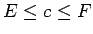 . Tā kā
. Tā kā
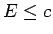 , tad
, tad 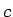 ir kopas
ir kopas  augšējā robeža, bet tā kā
augšējā robeža, bet tā kā 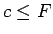 , tad
, tad 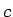 ir vismazākā starp kopas
ir vismazākā starp kopas  augšējām robežām. Seko,
ka
augšējām robežām. Seko,
ka 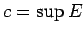 .
.
Analoģiski var pierādīt, ka katrai netukšai un ierobežotai no
apakšas kopai
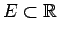 eksistē apakšējais slieksnis.
Tātad, ja kopa
eksistē apakšējais slieksnis.
Tātad, ja kopa
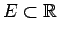 ir ierobežota
(ierobežota gan no apakšas, gan no augšas), tad tai eksistē gan
apakšējais, gan augšējais slieksnis.
ir ierobežota
(ierobežota gan no apakšas, gan no augšas), tad tai eksistē gan
apakšējais, gan augšējais slieksnis.
-
1.4. piez
 me.
me.
- Kopas sliekšņi var piederēt un var nepiederēt šai
kopai.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.4. Intervāli kopā
Augstāk: 1. REĀLO SKAITĻU KOPA
Iepriekšējais: 1.2. Reālā skaitļa modulis
2003-02-24
![]() ir ierobežota no
apakšas, bet nav ierobežota no augšas. Visu veselo skaitļu kopa
ir ierobežota no
apakšas, bet nav ierobežota no augšas. Visu veselo skaitļu kopa
![]() nav ierobežota ne no augšas, ne no apakšas.
nav ierobežota ne no augšas, ne no apakšas.
![]() , visu naturālo skaitļu kopa
, visu naturālo skaitļu kopa
![]() nav
ierobežotas kopas.
nav
ierobežotas kopas.
![]() kā
kopas
kā
kopas ![]() vismazāko augšējo robežu (lasa suprems1.14).
vismazāko augšējo robežu (lasa suprems1.14).
![]() Tā kā kopa
Tā kā kopa ![]() ir ierobežota no augšas, tad
tai eksistē augšējā robeža. Apzīmēsim ar
ir ierobežota no augšas, tad
tai eksistē augšējā robeža. Apzīmēsim ar ![]() kopas
kopas ![]() visu
augšējo robežu kopu. Acīmredzot,
visu
augšējo robežu kopu. Acīmredzot,
![]() un
un ![]() .
Saskaņā ar
.
Saskaņā ar
![]() nepārtrauktības Dedekinda
aksiomu
eksistē tāds skaitlis
nepārtrauktības Dedekinda
aksiomu
eksistē tāds skaitlis ![]() , ka
, ka
![]() . Tā kā
. Tā kā
![]() , tad
, tad ![]() ir kopas
ir kopas ![]() augšējā robeža, bet tā kā
augšējā robeža, bet tā kā ![]() , tad
, tad ![]() ir vismazākā starp kopas
ir vismazākā starp kopas ![]() augšējām robežām. Seko,
ka
augšējām robežām. Seko,
ka ![]() .
.
![]()