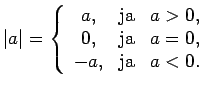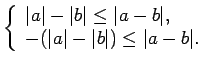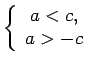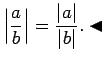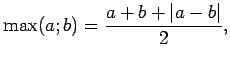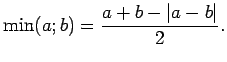Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.3. Reālo skaitļu kopas R ierobežotas kopas
Augstāk: 1. REĀLO SKAITĻU KOPA
Iepriekšējais: 1.1. Reālo skaitļu kopa un tās
Kopa
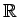 ir lineāri sakārtota kopa, t.i., apgalvojumi
ir lineāri sakārtota kopa, t.i., apgalvojumi
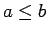 vai
vai 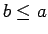 ir spēkā jebkuriem skaitļiem
ir spēkā jebkuriem skaitļiem  un
un 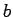 .
Ar
.
Ar
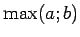 sapratīsim lielāko (bet ar
sapratīsim lielāko (bet ar 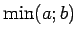 - mazāko)
no šiem skaitļiem. (Tajā gadījumā, kad šie skaitļi ir vienādi, ar
- mazāko)
no šiem skaitļiem. (Tajā gadījumā, kad šie skaitļi ir vienādi, ar
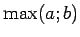 vai
vai 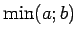 sapratīsim to kopīgo vērtību).
sapratīsim to kopīgo vērtību).
Acīmredzami,
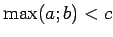 tad un tikai tad, kad
tad un tikai tad, kad 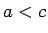 un
un 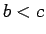 .
.
-
1.1. definīcija. 1.9
- Par reālā skaitļa
 moduli1.10 (absolūto vērtību)
nosauksim
moduli1.10 (absolūto vērtību)
nosauksim
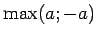 un apzīmēsim
un apzīmēsim 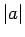 .
.
Seko, ka
Tā kā
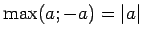 , tad
, tad 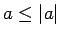 un
un 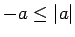 . No tā seko,
ka
. No tā seko,
ka
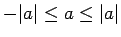 .
.
Moduļa īpašības
-
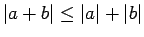 .
.
 Tā kā
Tā kā
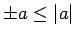 un
un
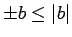 ,
tad
,
tad
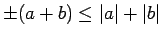 . Tātad
. Tātad
- Piezīme.
- Ar matemātiskās indukcijas1.11 metodi var pamatot, ka
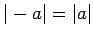 .
.
- Piezīme.
- Tātad
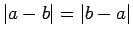 . Skaitli
. Skaitli 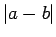 sauc par attālumu starp skaitļiem
sauc par attālumu starp skaitļiem  un
un 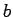 .
.
-
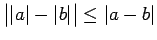 .
.
 Acīmredzami,
Acīmredzami, 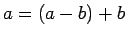 un
un 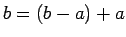 .
Saskaņā ar 1. īpašību
.
Saskaņā ar 1. īpašību
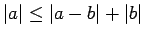 un
un
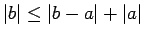 . Seko, ka
. Seko, ka
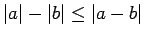 un
un
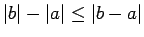 , t.i.,
Tātad
, t.i.,
Tātad
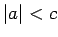 tad un tikai tad, kad
tad un tikai tad, kad 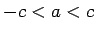 .
.
 Pirmkārt,
Pirmkārt, 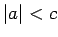 nozīmē, ka
nozīmē, ka 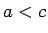 un
un
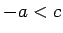 . Tātad
jeb
Otrkārt,
. Tātad
jeb
Otrkārt, 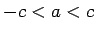 nozīmē, ka
nozīmē, ka 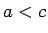 un
un 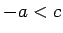 . Tātad
. Tātad 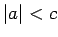 .
.
- Piezīme.
- Gadījumus
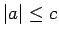 ,
, 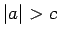 ,
, 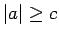 formulēt un pamatot patstāvīgi.
formulēt un pamatot patstāvīgi.
-
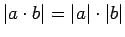 .
.
 Reizinājums
Reizinājums
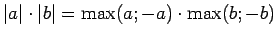 būs vienāds ar
būs vienāds ar 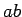 vai
vai
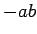 . Tā kā
. Tā kā
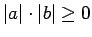 , tad
, tad
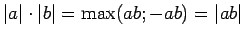 .
.
- Piezīme.
- Ar matemātiskās indukcijas metodi var
pamatot, ka
-
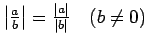 .
.
 Acīmredzami,
Acīmredzami,
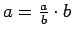 . Saskaņā
ar 5. īpašību
. Saskaņā
ar 5. īpašību
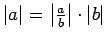 . Tātad
. Tātad
- Piezīme.
- Ar tiešo pārbaudi var pārliecināties, ka



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.3. Reālo skaitļu kopas R ierobežotas kopas
Augstāk: 1. REĀLO SKAITĻU KOPA
Iepriekšējais: 1.1. Reālo skaitļu kopa un tās
2003-02-24
![]() ir lineāri sakārtota kopa, t.i., apgalvojumi
ir lineāri sakārtota kopa, t.i., apgalvojumi
![]() vai
vai ![]() ir spēkā jebkuriem skaitļiem
ir spēkā jebkuriem skaitļiem ![]() un
un ![]() .
Ar
.
Ar
![]() sapratīsim lielāko (bet ar
sapratīsim lielāko (bet ar ![]() - mazāko)
no šiem skaitļiem. (Tajā gadījumā, kad šie skaitļi ir vienādi, ar
- mazāko)
no šiem skaitļiem. (Tajā gadījumā, kad šie skaitļi ir vienādi, ar
![]() vai
vai ![]() sapratīsim to kopīgo vērtību).
sapratīsim to kopīgo vērtību).