


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3. ROBEŽA
Augstāk: 2.4. Apvērsta funkcija
Iepriekšējais: 2.5. Jautājumi
- Nosaukt atbilstības un viennozīmīgas atbilstības piemērus.
- Izveidot brīvi izraudzītas funkcijas sašaurinājumu uz
kopu.
- Izveidot saliktas funkcijas piemēru un parādīt, ka divu
funkciju kompozīcija nav komutatīva.
- Izveidot bezgalīgi dilstošās ģeometriskās progresijas
piemēru un aprēķināt tās summu.
- Nosaukt stacionāru virkņu piemērus.
- Attēlot koordinātu plaknē un uz koordinātu taisnes
virknes
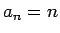 un
un
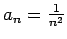 .
.
- Uzrakstīt kaut kādu virkni un izveidot divas tās
apakšvirknes.
- Nosaukt augošas un dilstošas funkcijas piemērus.
- Nosaukt kādu funkciju, kas nav monotona.
- Pierādīt, ka katra intervālā stingri monotona funkcija
ir injektīva funkcija šajā intervālā. Vai ir spēkā apgrieztais
apgalvojums?
- Pierādīt:
- ja funkcija
 aug, tad
aug, tad 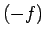 dilst;
dilst;
- ka divu augošu funkciju summa ir augoša funkcija;
- ka divu augošu funkciju reizinājums ir augoša
funkcija;
- ka divu augošu funkciju kompozīcija ir augoša
funkcija;
- ka divu dilstošu funkciju kompozīcija ir augoša
funkcija;
- ka augošas un dilstošas funkciju kompozīcija ir
dilstoša funkcija.
- Nosaukt ierobežotas no apakšas, ierobežotas no augšas,
ierobežotas funkciju piemērus.
- Nosaukt neierobežotas funkcijas piemērus.
- Pierādīt, ka funkcija
 ierobežota tad un tikai tad,
kad funkcija
ierobežota tad un tikai tad,
kad funkcija 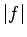 ierobežota no augšas2.20.
ierobežota no augšas2.20.
- Pierādīt, ka:
- divu pāra funkciju summa ir pāra funkcija;
- divu nepāra funkciju reizinājums ir pāra funkcija;
- pāra un nepāra funkcijas dalījums ir nepāra
funkcija.
- Pierādīt, ka katru funkciju, kurai definīcijas apgabals
ir simetrisks attiecībā pret koordinātu sākuma punktu, var
izteikt kā pāra un nepāra funkcijas summu.
- Nosaukt kādu funkciju, kas nav nedz pāra, nedz nepāra
funkcija.
- Nosaukt periodiskas, neperiodiskas funkcijas piemērus.
- Pierādīt, ka intervālā dilstoša funkcija ir apvēršama un
ka tās apvērstā funkcija arī ir dilstoša funkcija atbilstošajā
intervālā.
- Noskaidrot, kuras no šādām funkcijām ir apvēršamas
un kuras nē. Atbildi pamatot!
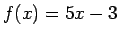 ;
;
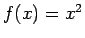 ;
;
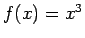 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3. ROBEŽA
Augstāk: 2.4. Apvērsta funkcija
Iepriekšējais: 2.5. Jautājumi
2003-02-24
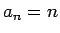 un
un
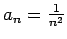 .
.
 aug, tad
aug, tad 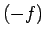 dilst;
dilst;
 ierobežota tad un tikai tad,
kad funkcija
ierobežota tad un tikai tad,
kad funkcija 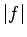 ierobežota no augšas2.20.
ierobežota no augšas2.20.
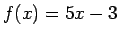 ;
;
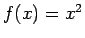 ;
;
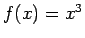 .
.