Pētot dažas funkcijas, bieži nākas risināt šādu uzdevumu: aprēķināt funkcijas
Pētot dažas funkcijas, bieži nākas risināt šādu uzdevumu:
aprēķināt funkcijas ![]() vērtību pēc dotās argumenta vērtības
vērtību pēc dotās argumenta vērtības
![]() . Daudzkārt ir jārisina arī apgrieztais uzdevums: atrast
argumenta vērtības, ar kurām funkcija
. Daudzkārt ir jārisina arī apgrieztais uzdevums: atrast
argumenta vērtības, ar kurām funkcija ![]() iegūst norādīto vērtību
iegūst norādīto vērtību
![]() .
.
Apskatīsim divus piemērus.
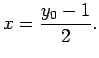
Tādējādi ![]() ir apvēršama funkcija, bet
ir apvēršama funkcija, bet ![]()
![]() nav apvēršama funkcija.
nav apvēršama funkcija.
No apvēršamas funkcijas definīcijas var izdarīt šādu secinājumu: ja funkcija
Pieņemsim, ka
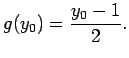
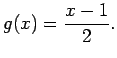
Tātad apvērsto funkciju ![]() var definēt tikai
apvēršamai funkcijai
var definēt tikai
apvēršamai funkcijai ![]() , pie tam
, pie tam ![]() un
un ![]() .
Funkcijas
.
Funkcijas ![]() apvērstā funkcija
apvērstā funkcija ![]() ir
vienīgā.
ir
vienīgā.
No funkcijas
No apvērstās funkcijas definīcijas izriet, ka ![]() ir vienāda ar
ir vienāda ar
![]() .
.
Tādējādi izvēloties citādu koordinātu sistēmu, kurā arguments tiek atlikts uz ordinātu ass, bet funkcijas vērtība uz abscisu ass, var uzskatīt, ka funkcijai
Ja funkcija ![]() aug (vai dilst) intervālā
aug (vai dilst) intervālā ![]() , tad šī funkcija
ir apvēršama. Funkcijas
, tad šī funkcija
ir apvēršama. Funkcijas ![]() apvērstā funkcija
apvērstā funkcija ![]() , kas
definēta kopā
, kas
definēta kopā ![]() , arī ir augoša (vai dilstoša).
, arī ir augoša (vai dilstoša).
![]() Apskatīsim tikai gadījumu, kad
Apskatīsim tikai gadījumu, kad ![]() ir
intervālā
ir
intervālā ![]() augoša funkcija. Vispirms pierādīsim, ka šī funkcija
ir apvēršama, t.i., kādu arī neizvēlētos skaitli
augoša funkcija. Vispirms pierādīsim, ka šī funkcija
ir apvēršama, t.i., kādu arī neizvēlētos skaitli ![]() no
funkcijas
no
funkcijas ![]() vērtībām, ko tā iegūst, ja
vērtībām, ko tā iegūst, ja ![]() pieder intervālam
pieder intervālam
![]() , šajā intervālā vienādojumam
, šajā intervālā vienādojumam ![]() ir vienīgais
atrisinājums
ir vienīgais
atrisinājums ![]() . Pieņemsim, ka intervālā
. Pieņemsim, ka intervālā ![]() ir vēl viens tāds
skaitlis
ir vēl viens tāds
skaitlis ![]() , ka
, ka
![]() . Tādā gadījumā
. Tādā gadījumā ![]() vai
vai
![]() . Funkcija
. Funkcija ![]() intervālā
intervālā ![]() ir augoša, tāpēc
ir augoša, tāpēc ![]() vai
vai
![]() , kas ir pretrunā ar vienādību
, kas ir pretrunā ar vienādību ![]() . Tāpēc
pieņēmums ir nepareizs un intervālā
. Tāpēc
pieņēmums ir nepareizs un intervālā ![]() skaitlis
skaitlis ![]() ir
vienādojuma
ir
vienādojuma ![]() vienīgā sakne. Tātad
vienīgā sakne. Tātad ![]() ir apvēršama
funkcija. Atliek pierādīt, ka funkcijas
ir apvēršama
funkcija. Atliek pierādīt, ka funkcijas ![]() apvērstā funkcija
apvērstā funkcija
![]() aug kopā
aug kopā ![]() . Pieņemsim, ka
. Pieņemsim, ka ![]() un
un ![]() ir brīvi
izraudzītas vērtības no kopas
ir brīvi
izraudzītas vērtības no kopas ![]() , turklāt
, turklāt ![]() un
un
![]() ,
,
![]() . Pieņemsim, ka
. Pieņemsim, ka
![]() . Pēc
apvērstās funkcijas definīcijas
. Pēc
apvērstās funkcijas definīcijas
![]() un
un
![]() .
Ievērojot, ka
.
Ievērojot, ka ![]() ir augoša funkcija un pēc pieņēmuma
ir augoša funkcija un pēc pieņēmuma
![]() , iegūsim, ka
, iegūsim, ka
![]() , t.i.,
, t.i.,
![]() , kas ir
pretrunā ar pieņēmumu
, kas ir
pretrunā ar pieņēmumu ![]() . Tāpēc atliek secināt, ka
. Tāpēc atliek secināt, ka
![]() , t.i.,
, t.i.,
![]() . Funkcija
. Funkcija ![]() aug kopā
aug kopā ![]() .
.
![]()