Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.3. Reālā mainīgā reālu funkciju klasifikācija
Augstāk: 2. FUNKCIJA
Iepriekšējais: 2.1. Funkcijas jēdziens
Ar reāliem skaitļiem ir definētas četras algebriskas darbības.
Rodas iespēja šīs darbības definēt arī ar
funkcijām2.11.
-
2.7. definīcija.
- Par divu funkciju
 un
un 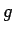 summu (apzīmēsim
summu (apzīmēsim
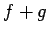 ) nosauksim funkciju, kurai:
) nosauksim funkciju, kurai:
-
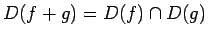 ;
;
- visiem
 no funkcijas
no funkcijas 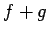 definīcijas apgabala
definīcijas apgabala
Līdzīgā veidā var definēt divu funkciju starpību un reizinājumu.
-
2.8. definīcija.
- Par divu funkciju
 un
un 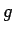 dalījumu (apzīmēsim
dalījumu (apzīmēsim
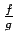 ) nosauksim funkciju, kurai:
) nosauksim funkciju, kurai:
-
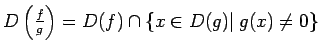 ;
;
- visiem
 no funkcijas
no funkcijas
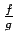 definīcijas
apgabala
definīcijas
apgabala
-
2.9. definīcija.
- Par funkcijas
 moduli (apzīmēsim
moduli (apzīmēsim 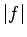 )
nosauksim funkciju, kurai:
)
nosauksim funkciju, kurai:
-
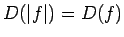 ;
;
- visiem
 no šo funkciju definīcijas apgabala
no šo funkciju definīcijas apgabala
Funkcijas argumentu aizstājot ar jauna argumenta funkciju, iegūst
tā saucamo saliktu funkciju2.12.
Piemēram, 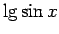 ,
, 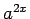 ir saliktas funkcijas. Ar saliktas
funkcijas definīcijas apgabalu sapratīsim to pēdējā
argumenta vērtības, kurām iegūtai izteiksmei ir jēga. Apskatīsim
divas funkcijas
ir saliktas funkcijas. Ar saliktas
funkcijas definīcijas apgabalu sapratīsim to pēdējā
argumenta vērtības, kurām iegūtai izteiksmei ir jēga. Apskatīsim
divas funkcijas 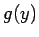 un
un 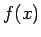 . Pirmās funkcijas argumenta
. Pirmās funkcijas argumenta 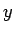 vietā rakstot
vietā rakstot 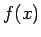 , iegūsim saliktu funkciju
, iegūsim saliktu funkciju
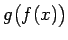 .
.
Šo saliktu funkciju vēl nosauksim par funkciju  un
un 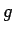 kompozīciju un apzīmēsim
kompozīciju un apzīmēsim 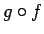 . Tātad
Tas nozīmē, ka saliktas funkcijas
. Tātad
Tas nozīmē, ka saliktas funkcijas
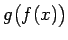 definīcijas
apgabals ir visu to funkcijas
definīcijas
apgabals ir visu to funkcijas  definīcijas apgabala punktu
definīcijas apgabala punktu  kopa, kuriem atbilstošās vērtības
kopa, kuriem atbilstošās vērtības 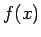 pieder funkcijas
pieder funkcijas 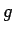 definīcijas apgabalam. Viegli var saskatīt, ka divu funkciju
kompozīcija nav komutatīva, t.i.,
definīcijas apgabalam. Viegli var saskatīt, ka divu funkciju
kompozīcija nav komutatīva, t.i.,
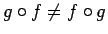 .
.
-
2.10. definīcija.
- Par virkni nosauksim funkciju2.13, kuras definīcijas apgabals ir visu naturālo skaitļu
kopa.
Šīs funkcijas vērtību punktā  apzīmēsim ar
apzīmēsim ar 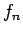 , bet pašu
virkni ar
, bet pašu
virkni ar 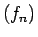 .
.
Pie fiksēta 
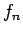 nosauksim par virknes
nosauksim par virknes
 -to locekli, bet pie patvaļīga
-to locekli, bet pie patvaļīga  -
virknes vispārīgo locekli.
-
virknes vispārīgo locekli.
Virkņu apzīmēšanai visbiežāk izmantosim latīņu alfabēta pirmos
burtus 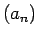 ,
, 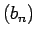 ,
, 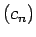 utt.
utt.
Virknes uzdod galvenokārt ar diviem paņēmieniem:
- ar
 -tā locekļa formulu;
-tā locekļa formulu;
- ar rekurences paņēmienu, kurā norāda pirmos
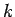 virknes
locekļus un formulu, saskaņā ar kuru var atrast šīs virknes
katru nākamo locekli. Piemēram,
virknes
locekļus un formulu, saskaņā ar kuru var atrast šīs virknes
katru nākamo locekli. Piemēram, 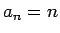 izsaka naturālo
skaitļu kopu. Rekurences formula
izsaka naturālo
skaitļu kopu. Rekurences formula
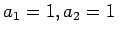
un
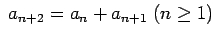
izsaka virkni
Skolā tiek apskatītas tādas skaitļu virknes kā aritmētiskā un
ģeometriskā progresija2.14.
Atgādinu, ka skaitļu virkni, kuras katrs loceklis, sākot no otrā,
vienāds ar iepriekšējā locekļa un viena un tā paša skaitļa 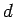 summu, sauc par aritmētisko progresiju. Skaitli
summu, sauc par aritmētisko progresiju. Skaitli 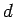 sauc par aritmētiskās progresijas diferenci. Aritmētisko
progresiju, kuras pirmais loceklis ir
sauc par aritmētiskās progresijas diferenci. Aritmētisko
progresiju, kuras pirmais loceklis ir 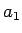 un diference
un diference 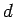 , var
definēt ar
, var
definēt ar 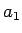 un rekurences formulu
un rekurences formulu
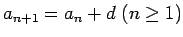 .
.
Skaitļu virkni, kuras pirmais loceklis nav vienāds ar nulli, bet
katrs loceklis, sākot no otrā, ir vienāds ar iepriekšējā
locekļa un no nulles atšķirīga skaitļa 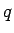 reizinājumu, sauc par
ģeometrisko progresiju. Skaitli
reizinājumu, sauc par
ģeometrisko progresiju. Skaitli 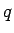 sauc par ģeometriskās
progresijas kvocientu. Ģeometrisko progresiju, kuras
pirmais loceklis ir
sauc par ģeometriskās
progresijas kvocientu. Ģeometrisko progresiju, kuras
pirmais loceklis ir 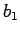 un kvocients ir
un kvocients ir 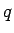 , var definēt ar
, var definēt ar
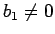 un rekurences formulu
un rekurences formulu
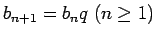 .
.
Virknes locekļi ir ne tikai tās vērtību kopas elementi, bet
elementi, kuriem ir piekārtoti numuri. Elementi var būt vienādi,
bet to numuri dažādi. Tādus elementus uzskatām par virknes
dažādiem locekļiem. Virknes vērtību kopa var sastāvēt pat no
viena elementa. Piemēram,
-
2.11. definīcija.
- Virkni nosauksim par stacionāru, ja tās
visu locekļu vērtības, sākot no kādas noteiktas vietas,
sakrīt.
Virknē 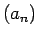 izsvītrosim tās locekļus tā, lai pāri paliktu
bezgalīgi daudz locekļu un šos pāri palikušos locekļus sanumurēsim
no jauna. Iegūsim jaunu virkni, kuru nosauksim par dotās virknes
izsvītrosim tās locekļus tā, lai pāri paliktu
bezgalīgi daudz locekļu un šos pāri palikušos locekļus sanumurēsim
no jauna. Iegūsim jaunu virkni, kuru nosauksim par dotās virknes
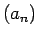 apakšvirkni un apzīmēsim
apakšvirkni un apzīmēsim
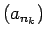 .
Elementu
.
Elementu 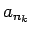 var iegūt no
var iegūt no 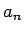 , ja
, ja  vietā ievieto
vietā ievieto 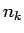 .
Tāpēc apakšvirkni var uzskatīt kā saliktu funkciju (divu funkciju
kompozīciju). Var runāt par virknes (kā funkcijas) grafiku
un to attēlot koordinātu plaknē.
.
Tāpēc apakšvirkni var uzskatīt kā saliktu funkciju (divu funkciju
kompozīciju). Var runāt par virknes (kā funkcijas) grafiku
un to attēlot koordinātu plaknē.
Šoreiz koordinātu plaknē iegūsim izolētus punktus. Virknei var
sniegt interpretāciju uz koordinātu taisnes, t.i., virknes
locekļus attēlot kā taisnes punktus.
Piemēram, apskatīsim virkni
Interpretēsim to koordinātu plaknē (2.8. zīm.) un uz
koordinātu taisnes (2.9. zīm.).



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.3. Reālā mainīgā reālu funkciju klasifikācija
Augstāk: 2. FUNKCIJA
Iepriekšējais: 2.1. Funkcijas jēdziens
2003-02-24
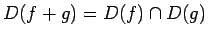 ;
;
 no funkcijas
no funkcijas 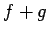 definīcijas apgabala
definīcijas apgabala
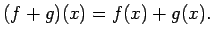
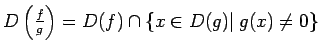 ;
;
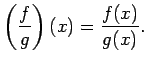
![]() izsvītrosim tās locekļus tā, lai pāri paliktu
bezgalīgi daudz locekļu un šos pāri palikušos locekļus sanumurēsim
no jauna. Iegūsim jaunu virkni, kuru nosauksim par dotās virknes
izsvītrosim tās locekļus tā, lai pāri paliktu
bezgalīgi daudz locekļu un šos pāri palikušos locekļus sanumurēsim
no jauna. Iegūsim jaunu virkni, kuru nosauksim par dotās virknes
![]() apakšvirkni un apzīmēsim
apakšvirkni un apzīmēsim
![]() .
Elementu
.
Elementu ![]() var iegūt no
var iegūt no ![]() , ja
, ja ![]() vietā ievieto
vietā ievieto ![]() .
Tāpēc apakšvirkni var uzskatīt kā saliktu funkciju (divu funkciju
kompozīciju). Var runāt par virknes (kā funkcijas) grafiku
un to attēlot koordinātu plaknē.
.
Tāpēc apakšvirkni var uzskatīt kā saliktu funkciju (divu funkciju
kompozīciju). Var runāt par virknes (kā funkcijas) grafiku
un to attēlot koordinātu plaknē.