


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.3.2. Ierobežotas funkcijas
Augstāk: 2.3. Reālā mainīgā reālu funkciju klasifikācija
Iepriekšējais: 2.3. Reālā mainīgā reālu funkciju klasifikācija
-
2.12. definīcija.
- Funkciju
 2.15 nosauksim par augošu kopā
2.15 nosauksim par augošu kopā
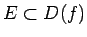 ,
ja visiem
,
ja visiem 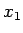 un
un 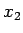 no
no  un kuriem
un kuriem 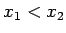 izpildās:
izpildās:
Līdzīgā veidā definē dilstošu, nedilstošu un neaugošu kopā  funkciju.
funkciju.
Par kopu  var būt šīs funkcijas definīcijas apgabals; šoreiz funkciju
sauc vienkārši, piemēram, par augošu.
var būt šīs funkcijas definīcijas apgabals; šoreiz funkciju
sauc vienkārši, piemēram, par augošu.
Visas šādas funkcijas (augošas, dilstošas, nedilstošas, neaugošas)
nosauksim par monotonām2.16 funkcijām, bet augošas vai
dilstošas par stingri monotonām.
Viegli saskatīt, ka, piemēram, nedilstošai funkcijai un, kas nav
augoša, ir tā saucamie pastāvīguma intervāli, t.i., intervāli,
kuros funkcija ir konstanta. Piemēram, funkcija 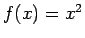 ir
augoša intervālā
ir
augoša intervālā
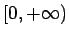 un dilstoša intervālā
un dilstoša intervālā
![$ (-\infty,
0]$](img277.gif) . Visā definīcijas apgabalā šī funkcija nav pat monotona.
(2.11. zīm.).
. Visā definīcijas apgabalā šī funkcija nav pat monotona.
(2.11. zīm.).



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.3.2. Ierobežotas funkcijas
Augstāk: 2.3. Reālā mainīgā reālu funkciju klasifikācija
Iepriekšējais: 2.3. Reālā mainīgā reālu funkciju klasifikācija
2003-02-24
![]() funkciju.
funkciju.