- ...
Dekarts1
- Renē Dekarts (1596-1650) - franču matemātiķis un
filozofs.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Paskāla2
- Blēzs Paskāls (1623-1662) - franču matemātiķis,
fiziķis un filozofs.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Fermā3
- Pjērs Fermā
(1601-1665) - franču matemātiķis un jurists.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... robežu1.1
- Uzskata, ka šāda robeža
eksistē.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...diferencējamu1.2
- Šis nosaukums radies no latīņu
valodas vārda ``diferentia", kas nozīmē ``starpība". Tiešām,
nosakot atvasinājumu, ir jāsastāda argumentam un
funkcijai vērtību starpības.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... kopa1.3
- Kopa
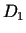 iekļaujas šīs funkcijas definīcijas apgabalā
iekļaujas šīs funkcijas definīcijas apgabalā 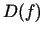 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
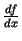 1.4
1.4
- Leibnics atvasinājumu
apzīmēja ar
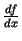 , bet vēlāk franču matemātiķis Ž ozefs
Luī Lagranžs (1736 - 1813) ieteica to apzīmēt ar
, bet vēlāk franču matemātiķis Ž ozefs
Luī Lagranžs (1736 - 1813) ieteica to apzīmēt ar 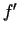 . Ņūtona
atvasinājuma apzīmējumu
. Ņūtona
atvasinājuma apzīmējumu 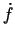 pašlaik matemātikā nelieto.
Tomēr mehānikā arī šodien atvasinājumu pēc laika mēdz
apzīmēt ar punktu.
pašlaik matemātikā nelieto.
Tomēr mehānikā arī šodien atvasinājumu pēc laika mēdz
apzīmēt ar punktu.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
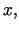 1.5
1.5
- Šo
vienādību var uzskatīt par punktā diferencējamas
funkcijas definīciju.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (skat. 1.6
- Izmantojot skaitļotāju, iegūsim, ka
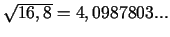
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... patstāvīgi1.7
- Pierāda, izmantojot atvasinājuma
definīciju.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...[Rolla2.1
- Mišels Rolls (1652-1719) - franču matemātiķis.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... nullēm2.2
- Par funkcijas nulli sauc
argumenta vērtību, kurai atbilstošā funkcijas vērtība ir vienāda
ar nulli.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... patstāvīgi.2.3
- Izveido palīgfunkciju
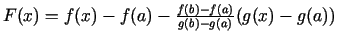 un šai
funkcijai pielieto Rolla teorēmu. Starpība
un šai
funkcijai pielieto Rolla teorēmu. Starpība
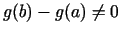 , jo
citādi atrastos tāds
, jo
citādi atrastos tāds
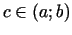 , ka
, ka 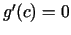 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Lopitāla2.4
- Gijoms Lopitāls (1661-1704) - franču
matemātiķis, pirmās iespiestās diferenciālrēķinu mācību grāmatas
autors. Šo kārtulu (metodi) atklāja šveiciešu matemātiķis Johans
Bernulli (1667-1748), bet 1696. gadā publicēja G. Lopitāls
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Teilora2.5
- Bruks Teilors (1685-1731) - angļu
matemātiķis.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... patstāvīgi3.1
- Sastādīt funkciju, kas ir doto
funkciju starpība, un tai pielietot 3.1. teorēmu
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
zīmi3.2
- Bieži ir noderīga tā saucamā intervālu metode.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...maksimuma3.3
- [lat. maximum - pats lielākais]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... minimuma3.4
- [lat. minimum - pats
mazākais]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...ekstrēma3.5
- [lat. extremum - galējs]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...stacionāro3.6
- [lat. stationarius - stāvošs, nekustīgs]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...kritiskajiem3.7
- izšķirošs,
lūzuma.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
patstāvīgi3.8
- Izmantojot funkcijas grafika pārliekuma punkta
definīciju; funkcijas grafika ieliekuma un izliekuma pietiekamo
nosacījumu.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... raksturīgos3.9
- grafika
krustpunkti ar asīm, ekstrēma un grafika pārliekuma punkti,
papildpunkti.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
teorēmu,4.1
- Uzskata, ka papildus funkcijas
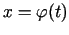 ,
,
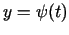 ir divreiz diferencējamas intervālā
ir divreiz diferencējamas intervālā  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... loku.4.2
- Parametrs
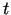 var
būt ne vien laiks, bet arī kāds cits fizikāls vai ģeometrisks
lielums.
var
būt ne vien laiks, bet arī kāds cits fizikāls vai ģeometrisks
lielums.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.