


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.3. Funkcijas ekstrēmi un to nepieciešamais
Augstāk: 3. ATVASINĀJUMA LIETOJUMI FUNKCIJU PĒTĪŠANĀ
Iepriekšējais: 3.1. Konstantas funkcijas nosacījums
3.2. teorēma. (Intervālā augošas funkcijas
nepieciešamais nosacījums). Ja intervālā  diferencējama
funkcija
diferencējama
funkcija  ir augoša, tad jebkurā šī intervāla punktā
ir augoša, tad jebkurā šī intervāla punktā
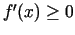 .
.
 Izvēlēsimies intervāla
Izvēlēsimies intervāla  patvaļīgu
punktu
patvaļīgu
punktu  un sastādīsim funkcijas
un sastādīsim funkcijas  pieaugumu šajā punktā
pieaugumu šajā punktā
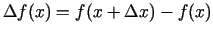 , kur
, kur
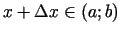 .
Intervālā augošai funkcijai tās pieauguma zīme sakrīt ar argumenta
pieauguma zīmi, tāpēc
.
Intervālā augošai funkcijai tās pieauguma zīme sakrīt ar argumenta
pieauguma zīmi, tāpēc
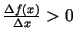 . Tā kā
. Tā kā  ir diferencējama funkcija, tad šādai attiecībai eksistē robeža,
kad
ir diferencējama funkcija, tad šādai attiecībai eksistē robeža,
kad
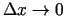 . Nevienādībā pārejot pie robežas,
iegūsim
. Nevienādībā pārejot pie robežas,
iegūsim
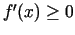 .
.
-
3.1. piezīme.
-

- Augošai funkcijai intervāla atsevišķos
punktos atvasinājums var būt nulle. Piemēram,
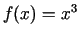 ir augoša
funkcija, bet
ir augoša
funkcija, bet 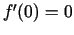 .
.
- Augošai funkcijai tie punkti, kuros atvasinājums ir
nulle, nedrīkst veidot nekādu intervālu. (Pretējā gadījumā šajā
intervālā funkcija būtu konstanta).
- Intervālā augošas funkcijas grafikam pieskares
veido ar abscisu ass pozitīvo virzienu šaurus leņķus vai
atsevišķos punktos ir paralēlas abscisu asij (3.1. zīm.).
Analogi var formulēt un pierādīt intervālā  dilstošas
funkcijas nepieciešamo nosacījumu.
dilstošas
funkcijas nepieciešamo nosacījumu.
3.3. teorēma. (Intervālā augošas funkcijas
pietiekamais nosacījums). Ja intervālā  diferencējamai
funkcijai katrā šī intervāla punktā
diferencējamai
funkcijai katrā šī intervāla punktā 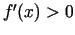 , tad
, tad  ir augoša
funkcija šajā intervālā.
ir augoša
funkcija šajā intervālā.
 Izvēlēsimies šī intervāla divus patvaļīgus
punktus
Izvēlēsimies šī intervāla divus patvaļīgus
punktus 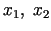 , pie tam
, pie tam 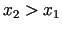 . Saskaņā ar Lagranža
formulu
. Saskaņā ar Lagranža
formulu
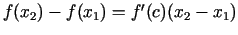 , kur
, kur 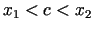 . Tā kā
visos intervāla
. Tā kā
visos intervāla  punktos
punktos 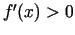 , tad arī
, tad arī 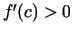 . Tā
kā
. Tā
kā 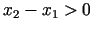 , tad arī
, tad arī
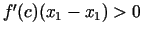 . Seko, ka
. Seko, ka
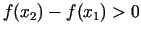 jeb
jeb
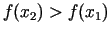 , t.i.,
, t.i.,  ir augoša
funkcija intervālā
ir augoša
funkcija intervālā  .
.
-
3.2. piezīme.
- Ja intervāla atsevišķos punktos
atvasinājums ir nulle, bet pārējos - pozitīvs, tad
 ir augoša
funkcija šajā intervālā.
ir augoša
funkcija šajā intervālā.
Analogi var formulēt un pierādīt intervālā  dilstošas
funkcijas pietiekamo nosacījumu.
dilstošas
funkcijas pietiekamo nosacījumu.
3.1. definīcija. Intervālus, kuros funkcija aug (vai dilst), sauc par
tās augšanas (vai dilšanas) intervāliem. Augšanas vai
dilšanas intervālus nešķirojot sauc par funkcijas monotonitātes intervāliem.
Lai atrastu funkcijas monotonitātes intervālus, rīkojas šādi.
- Atrod funkcijas atvasinājumu
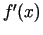 .
.
- Atrod tos intervālus, kuros atvasinājums saglabā
zīmi3.2. Ja
kādā intervālā
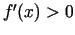 , tad tas ir funkcijas augšanas intervāls,
ja turpretim
, tad tas ir funkcijas augšanas intervāls,
ja turpretim 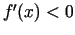 , tad - dilšanas intervāls.
, tad - dilšanas intervāls.
-
3.2. piemērs.
- Atrast funkcijas
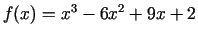 monotonitātes
intervālus.
monotonitātes
intervālus.
- Atrodam
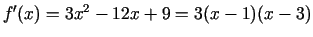 .
.
- Atvasinājums ir nulle punktos
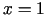 un
un 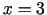 . Šie
punkti funkcijas definīcijas apgabalu sadala trijos intervālos.
Katrā no šiem intervāliem atvasinājums saglabā savu zīmi (lai
noteiktu atvasinājuma zīmi kādā no šiem intervāliem, pietiek
aprēķināt tā vērtību intervāla jebkurā vienā punktā). Atvasinājuma
vērtību zīmes ir lietderīgi atzīmēt uz skaitļu taisnes
(3.2. zīm.).
. Šie
punkti funkcijas definīcijas apgabalu sadala trijos intervālos.
Katrā no šiem intervāliem atvasinājums saglabā savu zīmi (lai
noteiktu atvasinājuma zīmi kādā no šiem intervāliem, pietiek
aprēķināt tā vērtību intervāla jebkurā vienā punktā). Atvasinājuma
vērtību zīmes ir lietderīgi atzīmēt uz skaitļu taisnes
(3.2. zīm.).
Tādējādi funkcijas augšanas intervāli ir
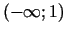 un
un
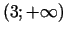 , bet dilšanas intervāls -
, bet dilšanas intervāls - 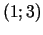 .
.
(Bultiņa uz augšu norāda, ka funkcija ir augoša, bet bultiņa uz
leju - ka funkcija ir dilstoša atbilstošajā intervālā). Funkcijas
grafiks attēlots 3.3. zīmējumā.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.3. Funkcijas ekstrēmi un to nepieciešamais
Augstāk: 3. ATVASINĀJUMA LIETOJUMI FUNKCIJU PĒTĪŠANĀ
Iepriekšējais: 3.1. Konstantas funkcijas nosacījums
2002-01-21
![]() diferencējama
funkcija
diferencējama
funkcija ![]() ir augoša, tad jebkurā šī intervāla punktā
ir augoša, tad jebkurā šī intervāla punktā
![]() .
.
![]() diferencējamai
funkcijai katrā šī intervāla punktā
diferencējamai
funkcijai katrā šī intervāla punktā ![]() , tad
, tad ![]() ir augoša
funkcija šajā intervālā.
ir augoša
funkcija šajā intervālā.