


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.2. Funkcijas monotonitātes nosacījumi
Augstāk: 3. ATVASINĀJUMA LIETOJUMI FUNKCIJU PĒTĪŠANĀ
Iepriekšējais: 3. ATVASINĀJUMA LIETOJUMI FUNKCIJU PĒTĪŠANĀ
3.1. teorēma. Lai funkcija  būtu konstanta
intervālā
būtu konstanta
intervālā  , ir nepieciešami un pietiekami, lai tai šajā
intervālā eksistētu atvasinājums, kas ir vienāds ar nulli.
, ir nepieciešami un pietiekami, lai tai šajā
intervālā eksistētu atvasinājums, kas ir vienāds ar nulli.
 Nepieciešamība. Izriet no
1.3. teorēmas.
Nepieciešamība. Izriet no
1.3. teorēmas.
Pietiekamība. Jebkuriem diviem šī intervāla punktiem  un
un  , kur
, kur  - fiksēts, bet
- fiksēts, bet  - patvaļīgs punkts, ir spēkā
Lagranža formula:
- patvaļīgs punkts, ir spēkā
Lagranža formula:
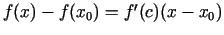 , kur
, kur 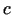 atrodas
starp
atrodas
starp  un
un  .
.
Tā kā 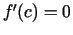 , tad
, tad
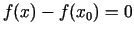 jeb
jeb
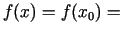 const. Tādējādi funkcija
const. Tādējādi funkcija  ir konstanta
intervālā
ir konstanta
intervālā  .
.
Sekas. Ja divām intervālā  diferencējamām funkcijām
ir vienādi atvasinājumi, tad šīs funkcijas var atšķirties tikai
par konstanti.
diferencējamām funkcijām
ir vienādi atvasinājumi, tad šīs funkcijas var atšķirties tikai
par konstanti.
Pierādīt patstāvīgi3.1.
-
3.1. piemērs.
- Pierādīt, ka
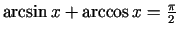 .
.
Izveidosim divas
funkcijas
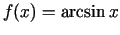 un
un
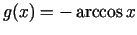 .
Acīmredzami, visiem
.
Acīmredzami, visiem
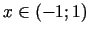 ir spēkā
ir spēkā
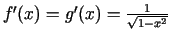 . Saskaņā ar sekām
. Saskaņā ar sekām
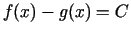 jeb
jeb
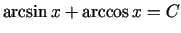 . Lai atrastu konstantes
vērtību, ievietosim šajā identitātē
. Lai atrastu konstantes
vērtību, ievietosim šajā identitātē 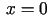 . Iegūsim
. Iegūsim
 jeb
jeb
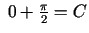 . Tādējādi
. Tādējādi
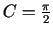 un
un
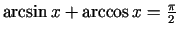 . Ar tiešo
pārbaudi var pārliecināties, ka vienādība ir spēkā arī šī
intervāla galapunktos.
. Ar tiešo
pārbaudi var pārliecināties, ka vienādība ir spēkā arī šī
intervāla galapunktos.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.2. Funkcijas monotonitātes nosacījumi
Augstāk: 3. ATVASINĀJUMA LIETOJUMI FUNKCIJU PĒTĪŠANĀ
Iepriekšējais: 3. ATVASINĀJUMA LIETOJUMI FUNKCIJU PĒTĪŠANĀ
2002-01-21
![]() būtu konstanta
intervālā
būtu konstanta
intervālā ![]() , ir nepieciešami un pietiekami, lai tai šajā
intervālā eksistētu atvasinājums, kas ir vienāds ar nulli.
, ir nepieciešami un pietiekami, lai tai šajā
intervālā eksistētu atvasinājums, kas ir vienāds ar nulli.