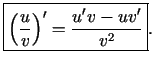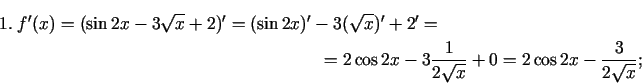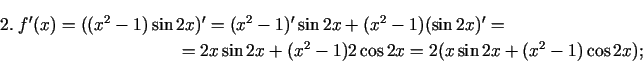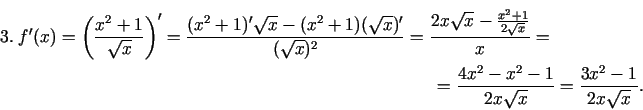Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.5. Saliktas funkcijas atvasinājums
Augstāk: 1. DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 1.3. Funkcijas diferenciālis un tā ģeometriskā
1.3. teorēma. Ja funkcija  ir konstanta kādā
intervālā
ir konstanta kādā
intervālā  , tad tās atvasinājums šajā intervālā ir nulle.
, tad tās atvasinājums šajā intervālā ir nulle.
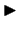 Tā kā visiem
Tā kā visiem
 ir spēkā
ir spēkā 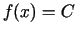 ,
tad
,
tad
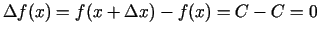 un
un
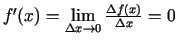 .
.
1.4. teorēma. Ja funkcijas 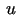 un
un 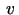 ir diferencējamas
punktā
ir diferencējamas
punktā 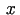 , tad
, tad
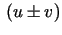 arī ir diferencējama šajā punktā, pie tam
arī ir diferencējama šajā punktā, pie tam
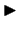 Sastādīsim funkcijas
Sastādīsim funkcijas 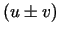 pieaugumu
punktā
pieaugumu
punktā 
Sastādīsim attiecību
Šīs vienādības labajai pusei eksistē galīga robeža, kad
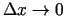 (jo funkcijas
(jo funkcijas 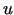 un
un 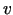 ir
diferencējamas punktā
ir
diferencējamas punktā  ), un tā ir vienāda ar
), un tā ir vienāda ar
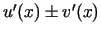 . Tas nozīmē, ka kreisajai pusei eksistē galīga
robeža, kas arī ir vienāda ar
. Tas nozīmē, ka kreisajai pusei eksistē galīga
robeža, kas arī ir vienāda ar
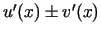 . Tādējādi
. Tādējādi 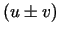 ir diferencējama punktā
ir diferencējama punktā  , pie tam
, pie tam
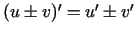 .
.
-
1.6. piezīme.
- Ar matemātiskās indukcijas metodi summas un
starpības atvasināšanas formulas var vispārināt jebkuram galīgam
funkciju skaitam.
1.5. teorēma. Ja funkcijas 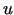 un
un 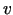 ir diferencējamas
punktā
ir diferencējamas
punktā  , tad
, tad 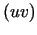 arī ir diferencējama šajā punktā,
pie tam
arī ir diferencējama šajā punktā,
pie tam
 Sastādīsim funkcijas
Sastādīsim funkcijas 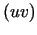 pieaugumu punktā
pieaugumu punktā

Sastādīsim attiecību
Šīs vienādības labajai pusei eksistē galīga robeža, kad
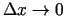 (jo
(jo 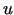 un
un 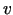 ir diferencējamas punktā
ir diferencējamas punktā
 un
un 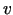 ir nepārtraukta šajā punktā kā diferencējama
funkcija), un tā ir vienāda ar
ir nepārtraukta šajā punktā kā diferencējama
funkcija), un tā ir vienāda ar
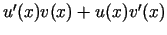 . Tas nozīmē,
ka kreisajai pusei eksistē galīga robeža, kas arī ir vienāda ar
. Tas nozīmē,
ka kreisajai pusei eksistē galīga robeža, kas arī ir vienāda ar
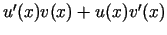 . Tādējādi
. Tādējādi 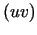 ir diferencējama
punktā
ir diferencējama
punktā  , pie tam
, pie tam
-
1.7. piezīme.
-

- Ar matemātiskās indukcijas metodi reizinājuma
atvasināšanas formulu var vispārināt jebkuram
galīgam funkciju skaitam. Piemēram,
- Apvienojot šo triju teorēmu rezultātus, var
teikt, ka jebkura galīga skaita diferencējamu funkciju
lineārā kombinācija ir diferencējama funkcija, pie
tam tās atvasinājums ir vienāds ar funkciju
atvasinājumu lineāro kombināciju. Piemēram, divu
funkciju gadījumā
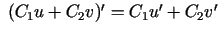 . Ja
. Ja
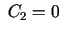 , tad iegūsim, ka
, tad iegūsim, ka
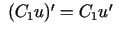 , t.i., ka konstantu
reizinātāju var iznest pirms atvasinājuma zīmes.
, t.i., ka konstantu
reizinātāju var iznest pirms atvasinājuma zīmes.
1.6. teorēma. Ja funkcijas 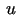 un
un 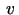 ir diferencējamas
punktā
ir diferencējamas
punktā 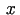 un
un
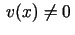 , tad
, tad
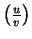 arī ir diferencējama šajā punktā, pie tam
arī ir diferencējama šajā punktā, pie tam
Pierādīt patstāvīgi1.7.
-
1.8. piemērs.
- Atvasināt šādas funkcijas:
-
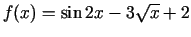 ;
;
-
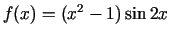 ;
;
-
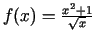 .
.
-
1.8. piezīme.
- Izmantojot diferencēšanas likumus un
funkcijas diferenciāļa definīciju, iegūst šādas formulas:
kur 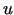 un
un 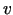 ir diferencējamas funkcijas.
ir diferencējamas funkcijas.
Piemēram,



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.5. Saliktas funkcijas atvasinājums
Augstāk: 1. DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 1.3. Funkcijas diferenciālis un tā ģeometriskā
2002-01-21
![]() ir konstanta kādā
intervālā
ir konstanta kādā
intervālā ![]() , tad tās atvasinājums šajā intervālā ir nulle.
, tad tās atvasinājums šajā intervālā ir nulle.
![]() un
un ![]() ir diferencējamas
punktā
ir diferencējamas
punktā ![]() , tad
, tad
![]() arī ir diferencējama šajā punktā, pie tam
arī ir diferencējama šajā punktā, pie tam
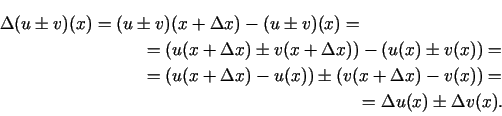
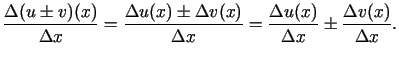
![]() un
un ![]() ir diferencējamas
punktā
ir diferencējamas
punktā ![]() , tad
, tad ![]() arī ir diferencējama šajā punktā,
pie tam
arī ir diferencējama šajā punktā,
pie tam
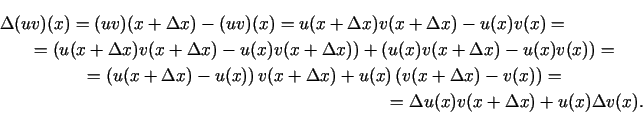
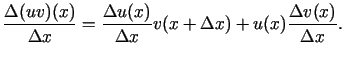
![]() un
un ![]() ir diferencējamas
punktā
ir diferencējamas
punktā ![]() un
un
![]() , tad
, tad
![]() arī ir diferencējama šajā punktā, pie tam
arī ir diferencējama šajā punktā, pie tam