


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.4. Diferencēšanas likumi
Augstāk: 1. DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 1.2. Funkcijas atvasinājuma ģeometriskā un fizikālā
Apskatīsim funkciju  , kas ir diferencējama punktā
, kas ir diferencējama punktā
 . Kā tika noskaidrots 1.2. teorēmas pierādījumā,
funkcijas pieaugumu šajā punktā var uzrakstīt šādi:
. Kā tika noskaidrots 1.2. teorēmas pierādījumā,
funkcijas pieaugumu šajā punktā var uzrakstīt šādi:
kur
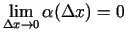 .
.
Kā redzams, funkcijas pieaugums ir divu saskaitāmo summa. Pirmais
saskaitāmais
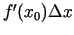 ir lineārs attiecībā pret
ir lineārs attiecībā pret 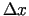 . Otrais saskaitāmais
. Otrais saskaitāmais
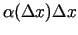 ir augstākas
kārtas bezgalīgi maza funkcija salīdzinājumā ar
ir augstākas
kārtas bezgalīgi maza funkcija salīdzinājumā ar 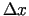 , kad
, kad
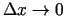 . Funkcijas pieaugumā noteicošā loma ir
pirmajam saskaitāmajam, tāpēc to uzskata par funkcijas pieauguma
galveno daļu.
. Funkcijas pieaugumā noteicošā loma ir
pirmajam saskaitāmajam, tāpēc to uzskata par funkcijas pieauguma
galveno daļu.
1.8. definīcija. Punktā  diferencējamas funkcijas
diferencējamas funkcijas  pieauguma šajā punktā galveno daļu, kas ir lineāra attiecībā pret
pieauguma šajā punktā galveno daļu, kas ir lineāra attiecībā pret
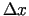 , sauc par šīs funkcijas diferenciāli punktā
, sauc par šīs funkcijas diferenciāli punktā  un apzīmē ar
un apzīmē ar 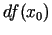 , t.i.,
, t.i.,
Mazām 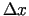 vērtībām funkcijas pieaugums
vērtībām funkcijas pieaugums
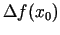 ir
aptuveni vienāds ar funkcijas pieauguma galveno daļu
ir
aptuveni vienāds ar funkcijas pieauguma galveno daļu
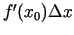 , t.i., funkcijas diferenciāli
, t.i., funkcijas diferenciāli 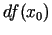 .
Tādējādi var rakstīt
.
Tādējādi var rakstīt
jeb
Šo aptuveno vienādību praktiski izmanto funkcijas vērtību
tuvinātā aprēķināšanā.
-
1.5. piezīme.
-

- Ja funkcijas diferenciāļa definīcijā
 vietā raksta
vietā raksta  un ar to saprot funkcijas definīcijas apgabala
patvaļīgu punktu, kurā šī funkcija ir diferencējama
(kopas
un ar to saprot funkcijas definīcijas apgabala
patvaļīgu punktu, kurā šī funkcija ir diferencējama
(kopas 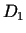 punkts), tad iegūst funkcijas diferenciāli
punkts), tad iegūst funkcijas diferenciāli 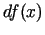 ,
kas ir atkarīgs gan no
,
kas ir atkarīgs gan no  , gan no
, gan no 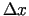 . Šoreiz
. Šoreiz
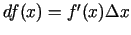 .
.
- Argumenta pieauguma
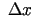 vietā parasti raksta
vietā parasti raksta 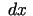 (argumenta diferenciālis). Šādos apzīmējumos
(argumenta diferenciālis). Šādos apzīmējumos
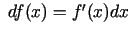 .
Tātad
.
Tātad
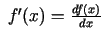 , kas ir gan funkcijas
atvasinājuma apzīmējums, gan funkcijas diferenciāļa un argumenta
diferenciāļa attiecība.
, kas ir gan funkcijas
atvasinājuma apzīmējums, gan funkcijas diferenciāļa un argumenta
diferenciāļa attiecība.
Apskatīsim dažus piemērus.
-
1.6. piemērs.
- Noteikt funkcijas
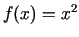 diferenciāli un
izskaitļot tā vērtību punktā
diferenciāli un
izskaitļot tā vērtību punktā 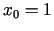 .
.
Sastādīsim šīs funkcijas pieaugumu
Acīmredzami, funkcijas pieauguma galvenā daļa ir
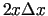 .
Seko, ka
.
Seko, ka
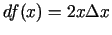 . (Vienlaicīgi esam sameklējuši arī šīs
funkcijas atvasinājumu, kas ir vienāds ar
. (Vienlaicīgi esam sameklējuši arī šīs
funkcijas atvasinājumu, kas ir vienāds ar 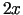 ).
).
Visbeidzot
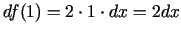 .
.
-
1.7. piemērs.
- Izmantojot funkcijas diferenciāli, izskaitļot
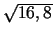 .
.
Izvēlēsimies funkciju
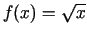 un
un 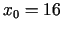 , šoreiz
, šoreiz
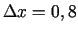 .
.
Izmantosim aptuveno vienādību
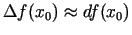 jeb
jeb
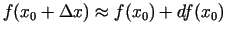 . Funkcijas diferenciāli
atradīsim kā funkcijas atvasinājuma un argumenta pieauguma
reizinājumu, t.i.,
. Funkcijas diferenciāli
atradīsim kā funkcijas atvasinājuma un argumenta pieauguma
reizinājumu, t.i.,
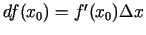 . Tā kā
. Tā kā
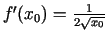 (skat. 1.2. piemēru),
tad
(skat. 1.2. piemēru),
tad
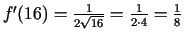 un
un
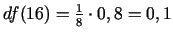 . Tātad
. Tātad
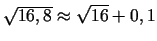 jeb
jeb
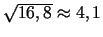 (skat. 1.6).
(skat. 1.6).
Lai noskaidrotu funkcijas  diferenciāļa
diferenciāļa 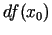 ģeometrisko
interpretāciju, koordinātu plaknē attēlosim šīs funkcijas grafiku
(1.6. zīm.).
Punktā
ģeometrisko
interpretāciju, koordinātu plaknē attēlosim šīs funkcijas grafiku
(1.6. zīm.).
Punktā
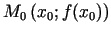 novilksim funkcijas grafikam
pieskari. Apzīmēsim ar
novilksim funkcijas grafikam
pieskari. Apzīmēsim ar 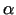 leņķi, ko veido pieskare ar
abscisu ass pozitīvo virzienu. Pieskares virziena koeficients
leņķi, ko veido pieskare ar
abscisu ass pozitīvo virzienu. Pieskares virziena koeficients
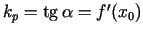 . Tā kā
. Tā kā
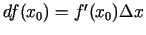 , tad
varam rakstīt
, tad
varam rakstīt
Tādējādi funkcijas  diferenciālis punktā
diferenciālis punktā  ir vienāds ar
šīs funkcijas grafikam punktā
ir vienāds ar
šīs funkcijas grafikam punktā
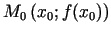 novilktās pieskares ordinātas pieaugumu (
novilktās pieskares ordinātas pieaugumu (
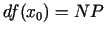 ). Tā arī ir
funkcijas diferenciāļa ģeometriskā interpretācija.
). Tā arī ir
funkcijas diferenciāļa ģeometriskā interpretācija.
Šajā zīmējumā funkcijas pieaugums punktā 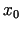
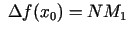 atšķiras no tās diferenciāļa
atšķiras no tās diferenciāļa
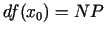 par
par
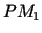 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.4. Diferencēšanas likumi
Augstāk: 1. DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 1.2. Funkcijas atvasinājuma ģeometriskā un fizikālā
2002-01-21
![]() diferencējamas funkcijas
diferencējamas funkcijas ![]() pieauguma šajā punktā galveno daļu, kas ir lineāra attiecībā pret
pieauguma šajā punktā galveno daļu, kas ir lineāra attiecībā pret
![]() , sauc par šīs funkcijas diferenciāli punktā
, sauc par šīs funkcijas diferenciāli punktā ![]() un apzīmē ar
un apzīmē ar ![]() , t.i.,
, t.i.,