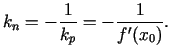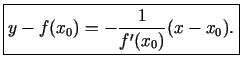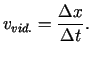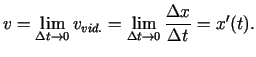Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.3. Funkcijas diferenciālis un tā ģeometriskā
Augstāk: 1. DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 1.1. Funkcijas atvasinājums
Apskatīsim funkciju  , kas ir nepārtraukta punktā
, kas ir nepārtraukta punktā  . Šādas
funkcijas grafiks attēlots 1.3. zīmējumā.
. Šādas
funkcijas grafiks attēlots 1.3. zīmējumā.
1.6. definīcija. Par funkcijas  grafika pieskari punktā
grafika pieskari punktā
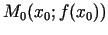 sauc taisni, kas iet caur šo punktu un kas
apmierina šādu nosacījumu: attālums
sauc taisni, kas iet caur šo punktu un kas
apmierina šādu nosacījumu: attālums 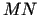 no grafika
patvaļīga punkta
no grafika
patvaļīga punkta 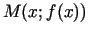 līdz šai taisnei ir pēc patikas mazs
salīdzinot ar attālumu
līdz šai taisnei ir pēc patikas mazs
salīdzinot ar attālumu 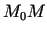 , kad
, kad  tiecas uz
tiecas uz  , t.i.,
, t.i.,
![$ \frac{MN}{M_0M}\xrightarrow[x\rightarrow x_0]{}0$](img85.gif) .
.
1.2. teorēma. Ja funkcija  -
diferencējama punktā
-
diferencējama punktā  , tad tās grafikam
atbilstošajā punktā
, tad tās grafikam
atbilstošajā punktā
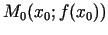 eksistē pieskare, kuras
vienādojums ir
eksistē pieskare, kuras
vienādojums ir
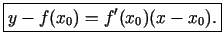 |
(1.1) |
 Tā kā funkcija
Tā kā funkcija  - diferencējama
punktā
- diferencējama
punktā  , tad tā ir nepārtraukta šajā punktā un eksistē galīgs
, tad tā ir nepārtraukta šajā punktā un eksistē galīgs
Saskaņā ar funkcijas robežu īpašībām
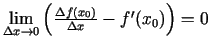 . Tas nozīmē, ka
. Tas nozīmē, ka
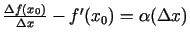 , kur
, kur 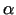 - bezgalīgi maza
funkcija, kad
- bezgalīgi maza
funkcija, kad 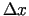 tiecas uz nulli. No šīs vienādības
iegūsim, ka
citiem
vārdiem,
tiecas uz nulli. No šīs vienādības
iegūsim, ka
citiem
vārdiem,
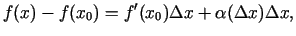 |
(1.2) |
kur
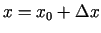 un
un
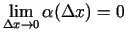 .
.
Acīmredzami, (1.1) ir taisnes, kas iet caur punktu
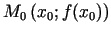 , vienādojums. Atliek pierādīt,
ka šī taisne ir funkcijas
, vienādojums. Atliek pierādīt,
ka šī taisne ir funkcijas  grafikam punktā
grafikam punktā 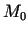 konstruētā
pieskare. Tam nolūkam ir jāparāda, ka izpildās nosacījums
konstruētā
pieskare. Tam nolūkam ir jāparāda, ka izpildās nosacījums
![$ \frac{MN}{M_0M}\xrightarrow[x\rightarrow x_0]{}0$](img85.gif) (1.3. zīm.). No vienādības (1.2) atņemsim (1.1)
un iegūsim:
(1.3. zīm.). No vienādības (1.2) atņemsim (1.1)
un iegūsim:
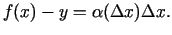 |
(1.3) |
Apskatīsim attiecību
Var saskatīt, ka
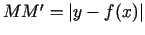 (situācijā, kas attēlota
1.3. zīmējumā,
(situācijā, kas attēlota
1.3. zīmējumā,
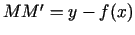 , jo punkta
, jo punkta 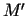 ordināta ir
ordināta ir
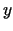 , bet punkta
, bet punkta 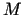 ordināta ir
ordināta ir 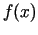 ). Atsaucoties uz vienādību
(1.3), var rakstīt, ka
Tāpēc
Acīmredzami,
). Atsaucoties uz vienādību
(1.3), var rakstīt, ka
Tāpēc
Acīmredzami,
![$ \frac{MN}{M_0M}\xrightarrow[x\rightarrow x_0]{}0$](img85.gif) , jo
, jo
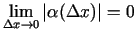 . Teorēma
ir pierādīta.
. Teorēma
ir pierādīta.
-
1.4. piezīme.
- Funkcijas
 grafikam punktā
grafikam punktā
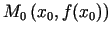 konstruētās pieskares virziena
koeficients
konstruētās pieskares virziena
koeficients
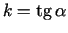 acīmredzami ir vienāds ar
acīmredzami ir vienāds ar 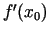 ,
t.i.,
,
t.i., 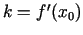 . No šejienes arī izriet funkcijas atvasinājuma ģeometriskā nozīme. Funkcijas
. No šejienes arī izriet funkcijas atvasinājuma ģeometriskā nozīme. Funkcijas  atvasinājums
punktā
atvasinājums
punktā  ir tās grafikam atbilstošajā punktā
ir tās grafikam atbilstošajā punktā
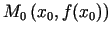 konstruētās pieskares virziena
koeficients (1.3. zīm.).
konstruētās pieskares virziena
koeficients (1.3. zīm.).
Ja funkcijai  punktā
punktā  ir bezgalīgs atvasinājums, tad
funkcijas grafikam atbilstošajā punktā
ir bezgalīgs atvasinājums, tad
funkcijas grafikam atbilstošajā punktā
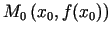 arī eksistē pieskare un tā ir
paralēla ordinātu asij; tās vienādojums ir
arī eksistē pieskare un tā ir
paralēla ordinātu asij; tās vienādojums ir 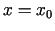 . Piemēram,
funkcijai
. Piemēram,
funkcijai
![$ f(x)=\sqrt[3]{x}$](img77.gif) punktā
punktā 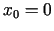 atvasinājums ir
bezgalīgs. Tās grafikam atbilstošajā punktā
atvasinājums ir
bezgalīgs. Tās grafikam atbilstošajā punktā 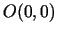 konstruētā
pieskare ir ordinātu ass. Pieskares vienādojums ir
konstruētā
pieskare ir ordinātu ass. Pieskares vienādojums ir 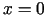 (1.4. zīm.).
(1.4. zīm.).
1.7. definīcija. Par funkcijas  grafika normāli punktā
grafika normāli punktā
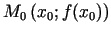 sauc taisni, kas iet caur šo punktu
un ir perpendikulāra šajā punktā konstruētajai pieskarei
(1.5. zīm.).
sauc taisni, kas iet caur šo punktu
un ir perpendikulāra šajā punktā konstruētajai pieskarei
(1.5. zīm.).
Tātad punktā 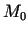 novilktā normāle un pieskare ir perpendikulāras
un pēc divu taišņu perpendikularitātes nosacījuma
novilktā normāle un pieskare ir perpendikulāras
un pēc divu taišņu perpendikularitātes nosacījuma
Tādējādi normāles vienādojums ir
-
1.5. piemērs.
- Sastādīt funkcijas
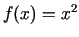 grafikam
punktā
grafikam
punktā 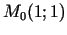 novilktās pieskares un normāles vienādojumus.
novilktās pieskares un normāles vienādojumus.
Saskaņā ar rezultātu, kas tika iegūts 1.1. piemērā,
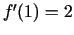 . Tādējādi
. Tādējādi 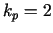 un
un
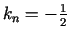 . Pieskares
vienādojums ir
. Pieskares
vienādojums ir
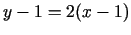 jeb
jeb 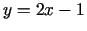 . Normāles vienādojums
. Normāles vienādojums
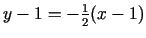 jeb
jeb
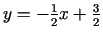 .
.
Noskaidrosim funkcijas atvasinājuma fizikālo interpretāciju.
Pieņemsim, ka materiālais punkts kustas nevienmērīgi pa taisni.
Kustības likums ir 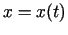 . Laika intervālā
. Laika intervālā
![$ [t;t+\Delta t]$](img126.gif) materiālā punkta pārvietojums ir
materiālā punkta pārvietojums ir
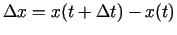 .
Kustības vidējo ātrumu
.
Kustības vidējo ātrumu 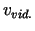 intervālā
intervālā
![$ [t;t+\Delta t]$](img126.gif) definē kā pārvietojuma attiecību pret kustības laiku, t.i.,
definē kā pārvietojuma attiecību pret kustības laiku, t.i.,
Lai raksturotu kustību laika momentā 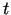 , izmanto momentānā ātruma
jēdzienu. Vidējā ātruma
, izmanto momentānā ātruma
jēdzienu. Vidējā ātruma 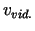 robežu, kad
robežu, kad
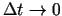 , sauc par momentāno ātrumu laika momentā
, sauc par momentāno ātrumu laika momentā
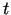 , t.i.,
, t.i.,
Tādējādi funkcijas atvasinājuma fizikālā (mehāniskā)
interpretācija ir momentānais ātrums taisnvirziena
kustībā.
Pēc analoģijas ar kustībā esošā materiālā punkta vidējo un
momentāno ātrumu funkcijas  pieauguma punktā
pieauguma punktā  un argumenta
pieauguma attiecību
un argumenta
pieauguma attiecību
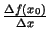 sauc par šīs
funkcijas maiņas vidējo ātrumu intervālā
sauc par šīs
funkcijas maiņas vidējo ātrumu intervālā
![$ [x_0;x_0+\Delta
x]$](img133.gif) . Funkcijas maiņas vidējā ātruma robežu, argumenta pieaugumam
tiecoties uz nulli, t.i.,
. Funkcijas maiņas vidējā ātruma robežu, argumenta pieaugumam
tiecoties uz nulli, t.i.,
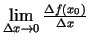 , vēl sauc par funkcijas
maiņas ātrumu punktā
, vēl sauc par funkcijas
maiņas ātrumu punktā  . Tādējādi funkcijas
. Tādējādi funkcijas  atvasinājums
punktā
atvasinājums
punktā  izsaka funkcijas maiņas ātrumu šajā punktā.
izsaka funkcijas maiņas ātrumu šajā punktā.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.3. Funkcijas diferenciālis un tā ģeometriskā
Augstāk: 1. DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 1.1. Funkcijas atvasinājums
2002-01-21
![\includegraphics[height=10cm]{C:/TEXfiles/vitolds/fun_lv_html/3arma.eps}](img80.gif)
![]() grafika pieskari punktā
grafika pieskari punktā
![]() sauc taisni, kas iet caur šo punktu un kas
apmierina šādu nosacījumu: attālums
sauc taisni, kas iet caur šo punktu un kas
apmierina šādu nosacījumu: attālums ![]() no grafika
patvaļīga punkta
no grafika
patvaļīga punkta ![]() līdz šai taisnei ir pēc patikas mazs
salīdzinot ar attālumu
līdz šai taisnei ir pēc patikas mazs
salīdzinot ar attālumu ![]() , kad
, kad ![]() tiecas uz
tiecas uz ![]() , t.i.,
, t.i.,
![]() .
.
![]() -
diferencējama punktā
-
diferencējama punktā ![]() , tad tās grafikam
atbilstošajā punktā
, tad tās grafikam
atbilstošajā punktā
![]() eksistē pieskare, kuras
vienādojums ir
eksistē pieskare, kuras
vienādojums ir
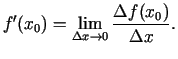
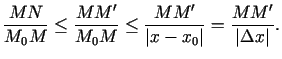
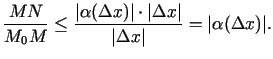
![]() grafika normāli punktā
grafika normāli punktā
![]() sauc taisni, kas iet caur šo punktu
un ir perpendikulāra šajā punktā konstruētajai pieskarei
(1.5. zīm.).
sauc taisni, kas iet caur šo punktu
un ir perpendikulāra šajā punktā konstruētajai pieskarei
(1.5. zīm.).