


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.2. Funkcijas atvasinājuma ģeometriskā un fizikālā
Augstāk: 1. DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 1. DIFERENCĒJAMAS FUNKCIJAS
Apskatīsim funkciju  , kas definēta punkta
, kas definēta punkta
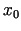 apkārtnē.
apkārtnē.
1.1. definīcija. Par funkcijas  atvasinājumu punktā
atvasinājumu punktā
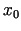 sauc šādu robežu1.1:
sauc šādu robežu1.1:
Funkcijas  atvasinājumu punktā
atvasinājumu punktā 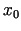 apzīmē ar
apzīmē ar 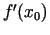 (lasa: "ef prim no
(lasa: "ef prim no 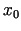 "). Saskaņā ar šo
definīciju
"). Saskaņā ar šo
definīciju
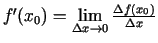 .
.
1.2. definīcija. Funkciju, kurai punktā 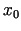 eksistē galīgs atvasinājums, sauc par diferencējamu1.2 jeb atvasināmu šajā
punktā.
eksistē galīgs atvasinājums, sauc par diferencējamu1.2 jeb atvasināmu šajā
punktā.
Pieņemsim, ka 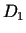 ir punktu kopa1.3, kurā
funkcija
ir punktu kopa1.3, kurā
funkcija  ir diferencējama. Katram skaitlim
ir diferencējama. Katram skaitlim
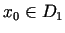 piekārtojot skaitli
piekārtojot skaitli
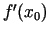 , iegūsim funkciju,
kas definēta kopā
, iegūsim funkciju,
kas definēta kopā 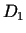 . Šo funkciju sauc par funkcijas
. Šo funkciju sauc par funkcijas  atvasināto funkciju jeb atvasinājumu un apzīmē ar
atvasināto funkciju jeb atvasinājumu un apzīmē ar
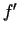 vai
vai
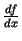 1.4 (attiecīgi lasa: "ef prim", "de ef pēc de
iks"). Lai, izmantojot atvasinājuma definīciju, noteiktu funkcijas
1.4 (attiecīgi lasa: "ef prim", "de ef pēc de
iks"). Lai, izmantojot atvasinājuma definīciju, noteiktu funkcijas
 atvasinājumu punktā
atvasinājumu punktā  , rīkojas šādi.
, rīkojas šādi.
- Izvēlas tādu argumenta pieaugumu
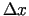 , ka
, ka
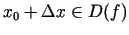 un sastāda tam atbilstošo funkcijas pieaugumu
punktā
un sastāda tam atbilstošo funkcijas pieaugumu
punktā  , t.i.,
, t.i.,
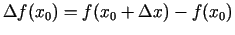 ;
;
- Sastāda funkcijas pieauguma punktā
 attiecību pret argumenta pieaugumu, t.i.,
attiecību pret argumenta pieaugumu, t.i.,
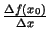 .
.
- Aprēķina attiecības
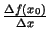 robežu, kad argumenta pieaugums
robežu, kad argumenta pieaugums
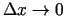 .
.
-
1.1. piezīme.
-

- Ja šādai attiecībai
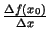 robeža neeksistē, tad punktā
robeža neeksistē, tad punktā  atvasinājums
neeksistē (funkcija nav diferencējama punktā
atvasinājums
neeksistē (funkcija nav diferencējama punktā  ).
).
- Ja
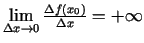 vai
vai
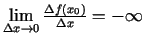 , tad saka, ka punktā
, tad saka, ka punktā  funkcijai
funkcijai
 ir bezgalīgs atvasinājums, un to pieraksta šādi:
ir bezgalīgs atvasinājums, un to pieraksta šādi:
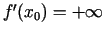 vai
vai
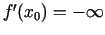 (arī šoreiz funkcija nav
diferencējama punktā
(arī šoreiz funkcija nav
diferencējama punktā  ).
).
- Ja punkts nav dots (šoreiz ir jāatrod funkcijas atvasinājums,
kas ir jauna kopā
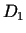 definēta funkcija), tad izvēlas funkcijas
definēta funkcija), tad izvēlas funkcijas
 definīcijas apgabala patvaļīgu iekšējo punktu
definīcijas apgabala patvaļīgu iekšējo punktu 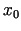 un,
rīkojoties pēc iepriekš minētās shēmas, atrod
un,
rīkojoties pēc iepriekš minētās shēmas, atrod 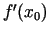 .
Visbeidzot, lai iegūtu atvasinājumu,
.
Visbeidzot, lai iegūtu atvasinājumu,  vietā raksta
vietā raksta
 , un ar to saprot patvaļīgu kopas
, un ar to saprot patvaļīgu kopas 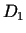 punktu.
punktu.
-
1.1. piemērs.
- Noteikt funkcijas
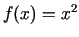 atvasinājumu
punktā
atvasinājumu
punktā 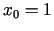 .
.
Rīkosimies pēc iepriekš minētās
shēmas.
Tādējādi 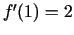 .
.
-
1.2. piemērs.
- Noteikt funkcijas
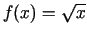 , atvasinājumu
punktā
, atvasinājumu
punktā 
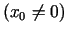 .
.
Tādējādi
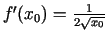 .
.
-
1.3. piemērs.
- Noteikt funkcijas
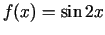 atvasinājumu.
atvasinājumu.
Tādējādi
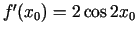 .
.
Visbeidzot
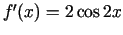 .
.
-
1.4. piemērs.
- Noteikt funkcijas
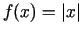 atvasinājumu.
atvasinājumu.
Izvēlēsimies  un tādu
un tādu  , ka
, ka
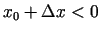 .
.
Tādējādi 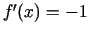
Visbeidzot 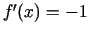 , ja
, ja 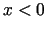 . Analogi
. Analogi 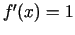 , ja
, ja 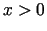 .
Acīmredzami
.
Acīmredzami
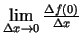 neeksistē, jo
neeksistē, jo
Tādējādi 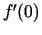 - neeksistē, citiem vārdiem, funkcija punktā
- neeksistē, citiem vārdiem, funkcija punktā
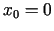 nav diferencējama.
nav diferencējama.
Tādējādi funkcijas 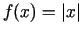 (1.1. zīm.) atvasinājums ir
definēts ar formulu
(1.1. zīm.) atvasinājums ir
definēts ar formulu
Pēc analoģijas ar funkcijas vienpusējām robežām tiek definēti arī
funkcijas vienpusējie atvasinājumi.
1.3. definīcija. Par funkcijas  atvasinājumu no labās (kreisās) puses
punktā
atvasinājumu no labās (kreisās) puses
punktā  sauc attiecības
sauc attiecības
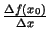 robežu, kad
robežu, kad 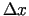 tiecas uz nulli no labās (kreisās) puses,
pieņemot, ka šāda robeža eksistē.
tiecas uz nulli no labās (kreisās) puses,
pieņemot, ka šāda robeža eksistē.
Funkcijas atvasinājumu no labās puses punktā
 apzīmē ar simbolu
apzīmē ar simbolu 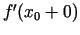 , bet no kreisās puses - ar
simbolu
, bet no kreisās puses - ar
simbolu 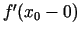 . Tādējādi
. Tādējādi
un
-
1.2. piezīme.
- No funkcijas robežas un tās vienpusējo robežu
definīcijām izriet, ka atvasinājums
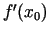 eksistē tad un tikai
tad, ja punktā
eksistē tad un tikai
tad, ja punktā  eksistē vienādi funkcijas
eksistē vienādi funkcijas  vienpusējie
atvasinājumi.
vienpusējie
atvasinājumi.
Piemēram, funkcijai 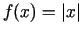 punktā
punktā 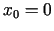 eksistē vienpusējie atvasinājumi, t.i.,
eksistē vienpusējie atvasinājumi, t.i.,
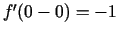 ,
, 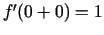 ,
bet tie nav vienādi. Tātad
,
bet tie nav vienādi. Tātad 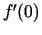 - neeksistē.
- neeksistē.
Sakaru starp diferencējamu un
nepārtrauktu funkciju izsaka šāda teorēma.
1.1. teorēma. Ja funkcija  ir diferencējama punktā
ir diferencējama punktā
 , tad tā ir nepārtraukta šajā punktā.
, tad tā ir nepārtraukta šajā punktā.
 Saskaņā ar doto eksistē galīgs
Saskaņā ar doto eksistē galīgs
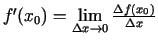 . Uzrakstīsim
acīmredzamu vienādību
. Uzrakstīsim
acīmredzamu vienādību
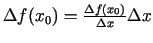
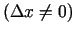 . Šajā vienādībā pāriesim
pie robežas, kad
. Šajā vienādībā pāriesim
pie robežas, kad 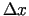 tiecas uz nulli. Iegūsim, ka
Seko, ka funkcija
tiecas uz nulli. Iegūsim, ka
Seko, ka funkcija  ir nepārtraukta punktā
ir nepārtraukta punktā  .
.
-
1.3. piezīme.
- Apgrieztā teorēma nav spēkā, t.i.,
vispārīgā gadījumā no funkcijas nepārtrauktības kādā
punktā neseko tās diferencējamība šajā punktā. Piemēram,
funkcija
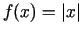 ir nepārtraukta punktā
ir nepārtraukta punktā 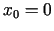 , bet
atvasinājums šajā punktā neeksistē. Apskatīsim vēl vienu piemēru.
Funkcija
, bet
atvasinājums šajā punktā neeksistē. Apskatīsim vēl vienu piemēru.
Funkcija
![$ f(x)=\sqrt[3]{x}$](img77.gif) ir nepārtraukta punktā
ir nepārtraukta punktā 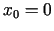 , bet
šajā punktā tā nav diferencējama, jo punktā
, bet
šajā punktā tā nav diferencējama, jo punktā 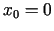 tai
neeksistē galīgs atvasinājums. Šoreiz
tai
neeksistē galīgs atvasinājums. Šoreiz
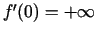 .
.
1.4. definīcija. Funkciju sauc par diferencējamu kopā 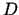 ,
ja tā ir diferencējama šīs kopas katrā punktā.
,
ja tā ir diferencējama šīs kopas katrā punktā.
1.5. definīcija. Funkciju, kas ir diferencējama savā
definīcijas apgabalā, sauc par diferencējamu
funkciju.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.2. Funkcijas atvasinājuma ģeometriskā un fizikālā
Augstāk: 1. DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 1. DIFERENCĒJAMAS FUNKCIJAS
2002-01-21
![]() atvasinājumu punktā
atvasinājumu punktā
![]() sauc šādu robežu1.1:
sauc šādu robežu1.1:
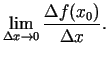
![]() eksistē galīgs atvasinājums, sauc par diferencējamu1.2 jeb atvasināmu šajā
punktā.
eksistē galīgs atvasinājums, sauc par diferencējamu1.2 jeb atvasināmu šajā
punktā.
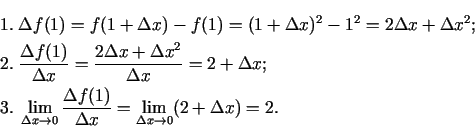
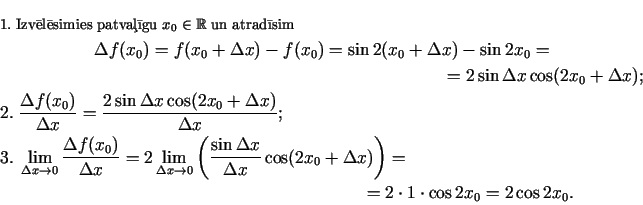
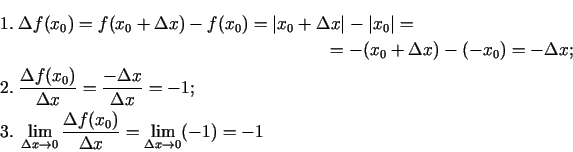
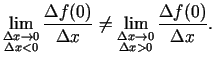
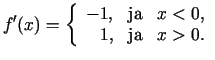
![]() atvasinājumu no labās (kreisās) puses
punktā
atvasinājumu no labās (kreisās) puses
punktā ![]() sauc attiecības
sauc attiecības
![]() robežu, kad
robežu, kad ![]() tiecas uz nulli no labās (kreisās) puses,
pieņemot, ka šāda robeža eksistē.
tiecas uz nulli no labās (kreisās) puses,
pieņemot, ka šāda robeža eksistē.
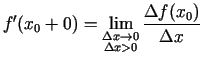
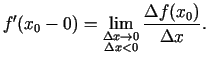
![]() ir diferencējama punktā
ir diferencējama punktā
![]() , tad tā ir nepārtraukta šajā punktā.
, tad tā ir nepārtraukta šajā punktā.
![]() ,
ja tā ir diferencējama šīs kopas katrā punktā.
,
ja tā ir diferencējama šīs kopas katrā punktā.