


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.6. Apvērstas funkcijas diferencēšana
Augstāk: 1. DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 1.4. Diferencēšanas likumi
Apskatīsim saliktu funkciju
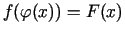 .
.
1.7. teorēma. Ja funkcija 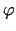 ir diferencējama punktā
ir diferencējama punktā
 un funkcija
un funkcija  ir diferencējama atbilstošajā punktā
ir diferencējama atbilstošajā punktā
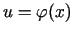 , tad salikta funkcija
, tad salikta funkcija 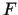 ir
diferencējama punktā
ir
diferencējama punktā  , pie tam
, pie tam
 Tā kā funkcija
Tā kā funkcija  ir
diferencējama punktā
ir
diferencējama punktā 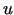 , tad tās pieaugumu šajā punktā
var uzrakstīt šādi:
, tad tās pieaugumu šajā punktā
var uzrakstīt šādi:
kur
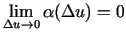 .
.
Izdalīsim vienādības abas puses ar
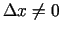 .
.
Tā kā
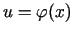 un
un
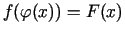 , tad šīs vienādības
kreisajā pusē var rakst
, tad šīs vienādības
kreisajā pusē var rakst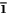 t
t
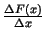 .
.
Iegūsim
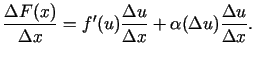 |
(1.4) |
Tā kā funkcija 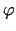 ir diferencējama punktā
ir diferencējama punktā  ,
tad eksistē galīga robeža
,
tad eksistē galīga robeža
un funkcija 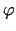 ir nepārtraukta punktā
ir nepārtraukta punktā  . Tāpēc
. Tāpēc
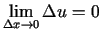 jeb
jeb
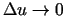 , ja
, ja
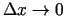 .
.
Vienādības (1.4) labajai pusei eksistē galīga robeža, kad
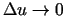 , un tā ir vienāda ar
, un tā ir vienāda ar
Tātad vienādības (1.4) kreisajai pusei eksistē galīga robeža
un tā ir vienāda ar
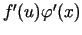 . Seko, ka funkcija
. Seko, ka funkcija  ir
diferencējama punktā
ir
diferencējama punktā  , pie tam
, pie tam
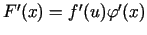 .
.
-
1.9. piemērs.
- Atvasināt funkciju
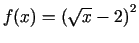 .
.
-
1.9. piezīme.
-

- Teorēmā minēto formulu bieži nākas
izmantot atkārtoti (ja starpargumentu skaits ir lielāks).
- Lietderīgi ievērot, ka saliktas funkcijas
atvasināšana notiek pretējā virzienā nekā šīs funkcijas vērtības
aprēķināšana. Piemēram, aplūkotajā piemērā aprēķinot funkcijas
vērtību, vispirms atrod
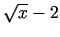 un tad iegūto skaitli kāpina
kvadrātā. Turpretī, atvasinot funkciju, rīkojas pretējā
secībā - vispirms atvasina pakāpi, ņemot vērā to, kādu izteiksmi
kāpina, un tikai tad atvasina pakāpes bāzi
un tad iegūto skaitli kāpina
kvadrātā. Turpretī, atvasinot funkciju, rīkojas pretējā
secībā - vispirms atvasina pakāpi, ņemot vērā to, kādu izteiksmi
kāpina, un tikai tad atvasina pakāpes bāzi
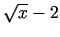 .
.
- Ja
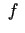 ir neatkarīgā mainīgā
ir neatkarīgā mainīgā 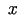 funkcija,
tad tās diferenciālis
funkcija,
tad tās diferenciālis
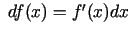 , kur
, kur
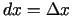 .
Turpretī, ja
.
Turpretī, ja  ir neatkarīgā mainīgā
ir neatkarīgā mainīgā 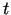 funkcija, t.i.,
funkcija, t.i.,
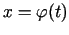 , tad
Tā kā
, tad
Tā kā
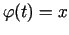 un
un
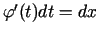 , tad var rakstīt, ka
arī šoreiz
, tad var rakstīt, ka
arī šoreiz
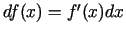 . Tādējādi funkcijas diferenciālim ir
tāda pati forma kā gadījumā, kad
. Tādējādi funkcijas diferenciālim ir
tāda pati forma kā gadījumā, kad  ir neatkarīgais mainīgais.
Citiem vārdiem, funkcijas diferenciāļa forma nav atkarīga no tā,
vai funkcijas arguments ir neatkarīgais mainīgais vai cita
argumenta funkcija. Šo īpašību sauc par diferenciāļa formas
invarianci (nemainīgumu).
ir neatkarīgais mainīgais.
Citiem vārdiem, funkcijas diferenciāļa forma nav atkarīga no tā,
vai funkcijas arguments ir neatkarīgais mainīgais vai cita
argumenta funkcija. Šo īpašību sauc par diferenciāļa formas
invarianci (nemainīgumu).



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.6. Apvērstas funkcijas diferencēšana
Augstāk: 1. DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 1.4. Diferencēšanas likumi
2002-01-21
![]() ir diferencējama punktā
ir diferencējama punktā
![]() un funkcija
un funkcija ![]() ir diferencējama atbilstošajā punktā
ir diferencējama atbilstošajā punktā
![]() , tad salikta funkcija
, tad salikta funkcija ![]() ir
diferencējama punktā
ir
diferencējama punktā ![]() , pie tam
, pie tam
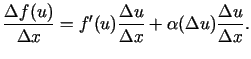
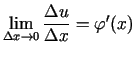
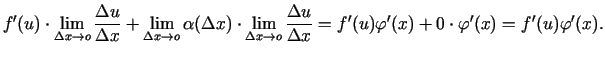
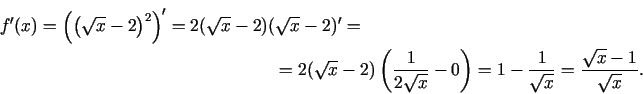
![$\displaystyle df\bigl(\varphi(t)\bigr)=\Bigl[f\bigl(\varphi(t)\bigr)\Bigr]'dt=f'(x)\varphi'(t)dt\/.$](img239.gif)