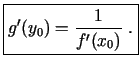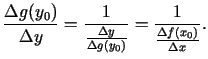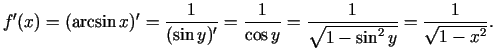Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.7. Elementāro pamatfunkciju atvasinājumi
Augstāk: 1. DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 1.5. Saliktas funkcijas atvasinājums
1.8. teorēma. Ja funkcija 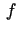 ir stingri monotona un nepārtraukta
intervālā
ir stingri monotona un nepārtraukta
intervālā 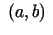 , ir diferencējama šī intervāla
punktā
, ir diferencējama šī intervāla
punktā 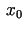 , pie tam
, pie tam
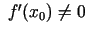 , tad tās apvērstā
funkcija
, tad tās apvērstā
funkcija 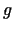 ir diferencējama atbilstošajā punktā
ir diferencējama atbilstošajā punktā
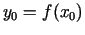 , pie tam
, pie tam
 Tā kā funkcija
Tā kā funkcija  ir stingri monotona un
nepārtraukta intervālā
ir stingri monotona un
nepārtraukta intervālā 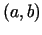 , tad tai eksistē apvērstā funkcija
, tad tai eksistē apvērstā funkcija
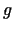 , kas arī ir nepārtraukta atbilstošajā intervālā.
, kas arī ir nepārtraukta atbilstošajā intervālā.
Izvēlēsimies argumenta  pieaugumu
pieaugumu 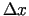 un tam atbilstošo
funkcijas
un tam atbilstošo
funkcijas  pieaugumu punktā
pieaugumu punktā  apzīmēsim ar
apzīmēsim ar
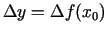 . Sastādīsim funkcijas
. Sastādīsim funkcijas 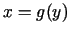 pieaugumu atbilstošajā
punktā
pieaugumu atbilstošajā
punktā
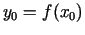 , kas atbilst argumenta
, kas atbilst argumenta 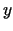 pieaugumam
pieaugumam 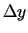 :
:
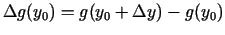 .
.
Izveidosim šādu attiecību
Šīs vienādības labajai pusei eksistē galīga robeža, kad
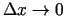 (jo funkcija
(jo funkcija  ir diferencējama punktā
ir diferencējama punktā
 un
un
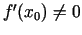 ), un šī robeža ir vienāda ar
), un šī robeža ir vienāda ar
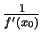 . Tas nozīmē, ka arī kreisajai pusei eksistē
galīga robeža, kas ir vienāda ar
. Tas nozīmē, ka arī kreisajai pusei eksistē
galīga robeža, kas ir vienāda ar
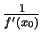 . Tādējādi
funkcija
. Tādējādi
funkcija 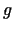 ir diferencējama atbilstošajā punktā
ir diferencējama atbilstošajā punktā 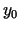 ,
pie tam
,
pie tam
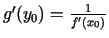 (Tā kā funkcijas
(Tā kā funkcijas  un
un 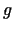 ir
nepārtrauktas atbilstoši punktos
ir
nepārtrauktas atbilstoši punktos  un
un 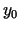 , tad
, tad
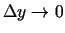 , kad
, kad
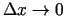 , un otrādi).
, un otrādi).
-
1.10. piemērs.
- Atvasināt funkciju
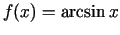 .
.
(Izmantojām, ka 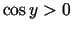 , jo šoreiz
, jo šoreiz
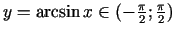 ).
).



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.7. Elementāro pamatfunkciju atvasinājumi
Augstāk: 1. DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 1.5. Saliktas funkcijas atvasinājums
2002-01-21
![]() ir stingri monotona un nepārtraukta
intervālā
ir stingri monotona un nepārtraukta
intervālā ![]() , ir diferencējama šī intervāla
punktā
, ir diferencējama šī intervāla
punktā ![]() , pie tam
, pie tam
![]() , tad tās apvērstā
funkcija
, tad tās apvērstā
funkcija ![]() ir diferencējama atbilstošajā punktā
ir diferencējama atbilstošajā punktā
![]() , pie tam
, pie tam