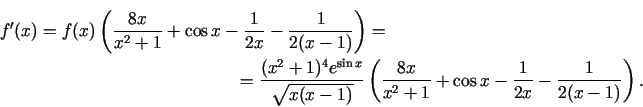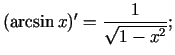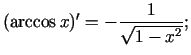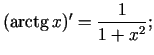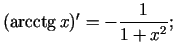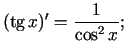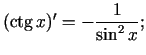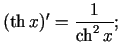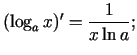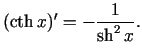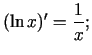Matemātika DU TSC
Nākamais: 1.8. Funkcijas augstāku kārtu atvasinājumi un Augstāk: 1. DIFERENCĒJAMAS FUNKCIJAS Iepriekšējais: 1.6. Apvērstas funkcijas diferencēšana

1.7. Elementāro pamatfunkciju atvasinājumi

Sastādīsim elementāro pamatfunkciju atvasinājumu tabulu.

$$1)\; (C)'=0; 9)\; (\arcsin x)'=\frac{1}{\sqrt{1-x^{2}}};$$

$$2)\; (x^{\alpha})'=\alpha x^{\alpha-1}; 10)\; (\arccos x)'=-\frac{1}{\sqrt{1-x^{2}}};$$

$$3)\; (\sin x)'=\cos x; 11)\; (\arctg x)'=\frac{1}{1+x^{2}};$$

$$4)\; (\cos x)'=-\sin x; 12)\; (\arctg x)'=-\frac{1}{1+x^{2}};$$

$$5)\; (\tg x)'=\frac{1}{\cos^{2}x}; 13)\; (\sh x)'=\ch x;$$

$$6)\; (\ctg x)'=-\frac{1}{\sin^{2}x}; 14)\; (\ch x)'=\sh x;$$

$$7)\; (a^{x})'=a^{x}\ln a; 15)\; (\Th x)'=\frac{1}{\ch^{2}x};$$

$$\; (e^{x})'=e^{x};$$

$$8)\; (\log_{a}x)'=\frac{1}{x\ln a}; 16)\; (\cth x)'=-\frac{1}{\sh^{2}x}.$$

$$\; (\ln x)'=\frac{1}{x};$$

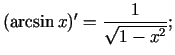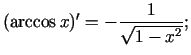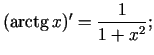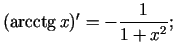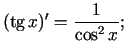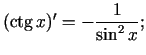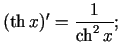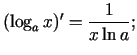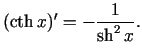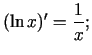Formulas 1. - 4. un 7. var pierādīt, izmantojot atvasinājuma definīciju, piemēram,

$$\begin{multline*} (a^{x})'=\lim\limits_{\Delta x\rightarrow 0}\frac{a^{x+\Delta ... ...lta x\rightarrow 0}\frac{a^{\Delta x}-1}{\Delta x}=a^{x}\ln a\/. \end{multline*}$$

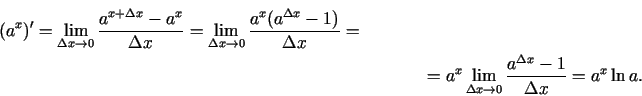
Formulas 5. un 6. var pierādīt, izmantojot atvasinājuma definīciju vai uzrakstot šīs funkcijas attiecīgi kā $\frac{\sin x}{\cos x}$ un $\frac{\cos x}{\sin x}$ un pēc tam atvasinot kā dalījumu. Piemēram,

$$\begin{multline*} (\tg x)'=\left(\frac{\sin x}{\cos x}\right)'=\frac{(\sin x)'\c... ...\\ =\frac{\cos^{2}x+\sin^{2}x}{\cos^{2}x}=\frac{1}{\cos^{2}x}\/. \end{multline*}$$

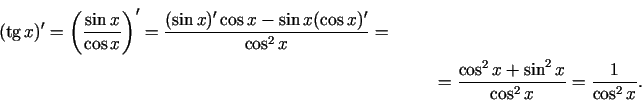
Formulu 8. var pierādīt, izmantojot atvasinājuma definīciju vai apvērstas funkcijas diferencēšanas formulu.

Formulas 9. - 12. pierāda, izmantojot apvērstas funkcijas diferencēšanas formulu.

Lai pierādītu formulas 13.-16., katru no šīm funkcijām uzraksta attiecīgi kā

$$\frac{e^{x}-e^{-x}}{2},\quad \frac{e^{x}+e^{-x}}{2},\quad \frac{\sh x}{\ch x},\quad \frac{\ch x}{\sh x}$$

un pēc tam atvasina, izmantojot diferencēšanas likumus.

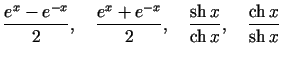
Lai atvasinātu funkciju $f(x)=u(x)^{v(x)}$, ir lietderīgi vispirms to uzrakstīt formā $e^{v(x)\ln u(x)}$ un atvasināt kā saliktu funkciju vai arī izmantot tā saucamo logaritmisko diferencēšanu. Logaritmiskās atvasināšanas algoritms ir šāds: vispirms logaritmē doto funkciju, piemēram, pie bāzes $e$, un tad atvasina iegūto vienādību.

1.11. piemērs. 

Atvasināt funkciju $f(x)=(x+1)^{\sin x}$.

1. paņēmiens.

$$f(x)=e^{\sin x\ln(x+1)}\/.$$

$$\begin{multline*} f'(x)=\left(e^{\sin x\ln(x+1)}\right)'=e^{\sin x\ln(x+1)}\left... ...x+1)^{\sin x}\left(\cos x\ln (x+1)+\frac{\sin x }{x+1}\right)\/; \end{multline*}$$

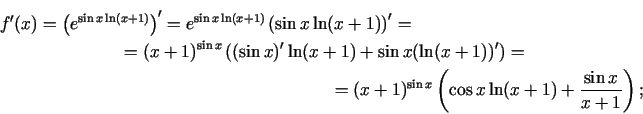
2. paņēmiens.

$$\ln f(x)=\sin x\ln (x+1)\/;$$

$$(\ln f(x))'=(\sin x\ln(x+1))'\/;$$

$$\frac{1}{f(x)}f'(x)=\cos x\ln(x+1)+\frac{\sin x}{x+1}\/;$$

$$\begin{multline*} f'(x)=f(x)\left(\cos x\ln(x+1)+\frac{\sin x}{x+1}\right)= \\ =... ...ft(\cos x\ln(x+1)+\frac{\sin x}{x+1}\right)\/.\qquad\qquad\qquad \end{multline*}$$

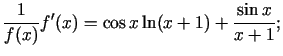
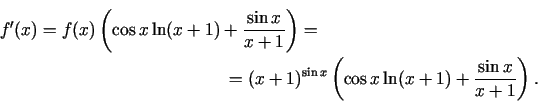
Logaritmisko atvasināšanu ir lietderīgi lietot arī tad, ja funkcijas izteiksmē ir vairāki reizinātāji vai dalītāji. Logaritmējot iegūst summu, kuras atvasinājumu var viegli atrast.

1.12. piemērs. 

Atvasināt funkciju $f(x)=\frac{\left(x^{2}+1\right)^{4}e^{\sin x}}{\sqrt{x(x-1)}}$.

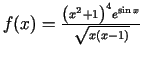Logaritmējam doto funkciju:

$$\ln f(x)=4\ln (x^{2}+1)+\sin x-\frac{1}{2}\ln x-\frac{1}{2}\ln (x-1)\/.$$

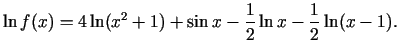
Atvasinām doto izteiksmi pēc $x$:

$$\frac{f'(x)}{f(x)}=\frac{8x}{x^{2}+1}+\cos x-\frac{1}{2x}-\frac{1}{2(x-1)}\/.$$

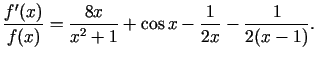
No šīs sakarības atrodam, ka

$$\begin{multline*} f'(x)=f(x)\left(\frac{8x}{x^{2}+1}+\cos x-\frac{1}{2x}-\frac{1... ...(\frac{8x}{x^{2}+1}+\cos x-\frac{1}{2x}-\frac{1}{2(x-1)}\right). \end{multline*}$$

Matemātika DU TSC
Nākamais: 1.8. Funkcijas augstāku kārtu atvasinājumi un Augstāk: 1. DIFERENCĒJAMAS FUNKCIJAS Iepriekšējais: 1.6. Apvērstas funkcijas diferencēšana