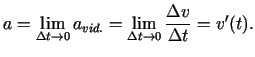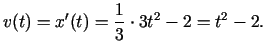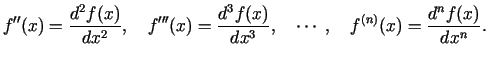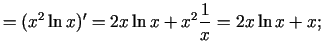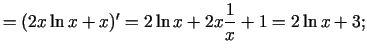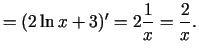Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.9. Jautājumi
Augstāk: 1. DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 1.7. Elementāro pamatfunkciju atvasinājumi
Pieņemsim, ka kopā 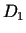 funkcijai
funkcijai  eksistē atvasinājums
eksistē atvasinājums
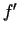 , kuru turpmāk sauksim arī par pirmās kārtas
atvasinājumu. Tas savukārt ir
, kuru turpmāk sauksim arī par pirmās kārtas
atvasinājumu. Tas savukārt ir  funkcija, tāpēc tam
var eksistēt atvasinājums, kuru sauksim par dotās funkcijas
funkcija, tāpēc tam
var eksistēt atvasinājums, kuru sauksim par dotās funkcijas  otrās kārtas atvasinājumu. Otrās kārtas
atvasinājumu apzīmē ar vienu no simboliem
otrās kārtas atvasinājumu. Otrās kārtas
atvasinājumu apzīmē ar vienu no simboliem 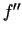 vai
vai
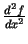 (attiecīgi lasa: "ef divi prim", "de
divi ef pēc de iks kvadrātā").
(attiecīgi lasa: "ef divi prim", "de
divi ef pēc de iks kvadrātā").
Analogi definē funkcijas trešās, ceturtās utt. kārtu
atvasinājumus, kurus attiecīgi apzīmē:
Vispār, par funkcijas
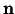 -tās kārtas
atvasinājumu sauc atvasinājumu no šīs
funkcijas
-tās kārtas
atvasinājumu sauc atvasinājumu no šīs
funkcijas 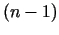 -ās kārtas atvasinājuma. Tādējādi
-ās kārtas atvasinājuma. Tādējādi
jeb
1.9. definīcija. Atvasinājumus, kuru kārta ir lielāka par
pirmo, sauc par augstāku kārtu atvasinājumiem.
-
1.13. piemērs.
- Noteikt funkcijas
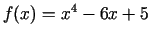 piektās
kārtas atvasinājumu.
piektās
kārtas atvasinājumu.
-
1.14. piemērs.
- Noteikt funkcijas
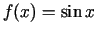
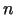 -tās
kārtas atvasinājumu.
-tās
kārtas atvasinājumu.
Noskaidrosim funkcijas otrās kārtas atvasinājuma mehānisko
interpretāciju. Ja 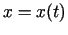 ir materiālā punkta
taisnvirziena kustības likums, tad
ir materiālā punkta
taisnvirziena kustības likums, tad
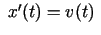 ir punkta
momentānais ātrums. Acīmredzot
ir punkta
momentānais ātrums. Acīmredzot
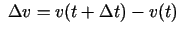 ir momentānā ātruma pieaugums laika intervālā
ir momentānā ātruma pieaugums laika intervālā 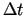 .
Attiecību
.
Attiecību
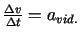 sauc par materiālā
punkta vidējo paātrinājumu intervālā
sauc par materiālā
punkta vidējo paātrinājumu intervālā 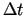 .
.
1.10. definīcija. Par materiālā punkta paātrinājumu
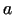 laika momentā
laika momentā 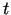 sauc vidējā paātrinājuma robežu, kad
sauc vidējā paātrinājuma robežu, kad
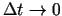 , t.i.,
, t.i.,
Tādējādi otrās kārtas atvasinājuma mehāniskā interpretācija
ir taisnvirziena kustībā esoša materiālā punkta momentānais
paātrinājums.
-
1.15. piemērs.
- Noteikt materiālā punkta ātrumu un
paātrinājumu laika momentā
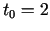 , ja kustības likums ir
, ja kustības likums ir
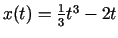 .
.
Momentānais ātrums 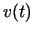 laika momentā
laika momentā 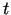 :
:
Laika momentā
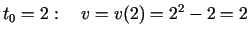 .
.
Momentānais paātrinājums 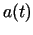 laika momentā
laika momentā 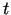 :
:
Laika momentā
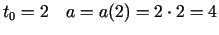 .
.
Pieņemsim, ka  ir kopā
ir kopā 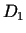 diferencējama funkcija
un
diferencējama funkcija
un
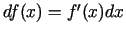 ir tās diferenciālis, kuru turpmāk sauksim par
pirmās kārtas diferenciāli.
ir tās diferenciālis, kuru turpmāk sauksim par
pirmās kārtas diferenciāli.
Pirmās kārtas diferenciālis ir atkarīgs gan no  , gan no
, gan no 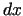 .
Ja
.
Ja 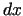 uzskata par nemainīgu, tad var teikt, ka pirmās kārtas
diferenciālis ir kopā
uzskata par nemainīgu, tad var teikt, ka pirmās kārtas
diferenciālis ir kopā 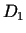 definēta
definēta  funkcija. Tāpēc tam var
eksistēt diferenciālis, kuru sauksim par dotās funkcijas
funkcija. Tāpēc tam var
eksistēt diferenciālis, kuru sauksim par dotās funkcijas  otrās kārtas diferenciāli. Otrās kārtas diferenciāli apzīmē ar
otrās kārtas diferenciāli. Otrās kārtas diferenciāli apzīmē ar
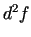 . Tādējādi
. Tādējādi
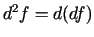 .
.
Vispār, par funkcijas
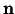 -tās kārtas diferenciāli
sauc diferenciāli no šīs funkcijas
-tās kārtas diferenciāli
sauc diferenciāli no šīs funkcijas 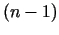 -ās kārtas diferenciāļa.
Tādējādi
-ās kārtas diferenciāļa.
Tādējādi
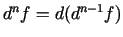 .
.
1.11. definīcija. Diferenciāļus, kuru kārta ir lielāka
par pirmo, sauc par augstāku kārtu diferenciāļiem.
Ja  ir neatkarīgais mainīgais un funkcijai
ir neatkarīgais mainīgais un funkcijai  eksistē
eksistē 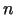 -tās
kārtas atvasinājums, tad, ievērojot, ka
-tās
kārtas atvasinājums, tad, ievērojot, ka 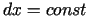 , iegūsim šādas
formulas:
, iegūsim šādas
formulas:
kur
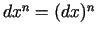 .
.
Izmantojot iegūtās formulas, rodas iespēja augstāku kārtu
atvasinājumus uzrakstīt kā diferenciāļu attiecības:
Ja  nav neatkarīgais mainīgais, tad saskaņā ar diferenciāļa
formas invarianci formula
nav neatkarīgais mainīgais, tad saskaņā ar diferenciāļa
formas invarianci formula
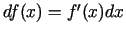 paliek spēkā. Atrodot
otrās kārtas diferenciāli,
paliek spēkā. Atrodot
otrās kārtas diferenciāli, 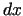 vairs nevar uzskatīt par
konstantu un ir jāizmanto reizinājuma diferenciāļa formula. Šoreiz
vairs nevar uzskatīt par
konstantu un ir jāizmanto reizinājuma diferenciāļa formula. Šoreiz
Analogi var atrast arī pārējos diferenciāļus.
-
1.10. piezīme.
- Augstāko kārtu diferenciāļiem vairs
nepiemīt to formas invariance.
-
1.16. piemērs.
- Noteikt funkcijas
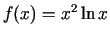 trešās
kārtas diferenciāli un izskaitļot to punktā
trešās
kārtas diferenciāli un izskaitļot to punktā 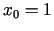 .
.
Izmantosim formulu
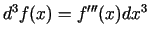 .
.
Atradīsim
Tādējādi
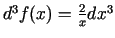 un
un
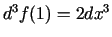 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.9. Jautājumi
Augstāk: 1. DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 1.7. Elementāro pamatfunkciju atvasinājumi
2002-01-21
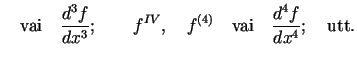
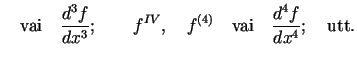
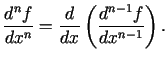
![]() laika momentā
laika momentā ![]() sauc vidējā paātrinājuma robežu, kad
sauc vidējā paātrinājuma robežu, kad
![]() , t.i.,
, t.i.,