nākamais augstāk iepriekšējais saturs Matemātika DU TSC
Nākamais: 1.10. Vingrinājumi Augstāk: 1. DIFERENCĒJAMAS FUNKCIJAS Iepriekšējais: 1.8. Funkcijas augstāku kārtu atvasinājumi un

1.9. Jautājumi

  1. Definēt funkcijas atvasinājumu punktā.
  2. Definēt punktā diferencējamu funkciju.
  3. Definēt funkcijas atvasinājumu.
  4. Sniegt funkcijas atvasinājuma atrašanas kārtulu, izmantojot tā definīciju.
  5. Kādos gadījumos funkcija nav diferencējama punktā?
  6. Definēt funkcijas atvasinājumu punktā no kreisās (labās) puses.
  7. Ko var pateikt par funkcijas vienpusējiem atvasinājumiem punktā, kurā funkcija ir diferencējama?
  8. Ko var pateikt par funkcijas vienpusējiem atvasinājumiem punktā, kurā funkcija nav diferencējama?
  9. Kāds sakars pastāv starp nepārtrauktu un diferencējamu punktā funkciju?
  10. Definēt kopā diferencējamu funkciju un definēt diferencējamu funkciju.
  11. Definēt funkcijas grafika pieskari.
  12. Kādai ir jābūt funkcijai, lai tās grafikam eksistētu pieskare?
  13. Uzrakstīt diferencējamas funkcijas grafika pieskares vienādojumu.
  14. Sniegt funkcijas atvasinājuma ģeometrisko interpretāciju.
  15. Ko var pateikt par funkcijas grafika pieskari, ja funkcijai atbilstošajā punktā eksistē bezgalīgs atvasinājums?
  16. Definēt funkcijas grafika normāli un uzrakstīt tās vienādojumu.
  17. Sniegt funkcijas atvasinājuma fizikālo interpretāciju.
  18. Definēt funkcijas diferenciāli punktā.
  19. Uzrakstīt funkcijas vērtības tuvinātās aprēķināšanas formulu.
  20. Sniegt funkcijas diferenciāļa ģeometrisko interpretāciju.
  21. Formulēt summas, reizinājuma un dalījuma diferencēšanas likumus.
  22. Uzrakstīt saliktas funkcijas atvasināšanas formulu.
  23. Formulēt funkcijas diferenciāļa invariances īpašību.
  24. Uzrakstīt apvērstas funkcijas atvasināšanas formulu.
  25. Nosaukt elementāro pamatfunkciju atvasinājumus.
  26. Formulēt logaritmiskās diferencēšanas algoritmu.
  27. Definēt funkcijas otrās kārtas un 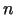$ n$-tās kārtas atvasinājumus.
  28. Sniegt funkcijas otrās kārtas atvasinājuma mehānisko interpretāciju.
  29. Definēt funkcijas otrās kārtas un 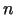$ n$-tās kārtas diferenciāļus.
  30. Uzrakstīt augstāku kārtu diferenciāļu izskaitļošanas formulas.
  31. Vai augstāku kārtu diferenciāļiem piemīt to formas invariance?

nākamais augstāk iepriekšējais saturs Matemātika DU TSC
Nākamais: 1.10. Vingrinājumi Augstāk: 1. DIFERENCĒJAMAS FUNKCIJAS Iepriekšējais: 1.8. Funkcijas augstāku kārtu atvasinājumi un

2002-01-21