


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2. DIFERENCIĀLRĒĶINU PAMATTEORĒMAS
Augstāk: 1. DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 1.9. Jautājumi
- Izmantojot atvasinājuma definīciju, atrast šādu
funkciju atvasinājumus:
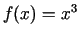 punktā
punktā 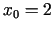 ;
;
-
![$ f(x)=\sqrt[3]{x}$](img77.gif) punktā
punktā 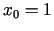 ;
;
-
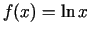 punktā
punktā  ;
;
-
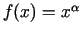 ;
;
-
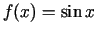 ;
;
-
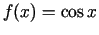 ;
;
-
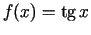 ;
;
-
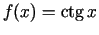 ;
;
-
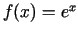 ;
;
-
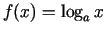 .
.
- Konstruēt funkciju, kurai punktā eksistē
bezgalīgs atvasinājums.
- Konstruēt funkciju, kurai punktā eksistē
galīgi vienpusējie atvasinājumi, bet kas nav
diferencējama šajā punktā.
- Konstruēt funkciju, kas ir nepārtraukta, bet nav
diferencējama šajā punktā.
- Minēt diferencējamu funkciju piemērus.
- Sastādīt funkcijas
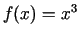 grafikam punktā,
kura abscisa ir
grafikam punktā,
kura abscisa ir 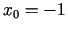 , novilktās pieskares un normāles
vienādojumus.
, novilktās pieskares un normāles
vienādojumus.
- Sastādīt funkcijas
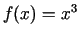 pieaugumu punktā
pieaugumu punktā
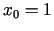 un noteikt tās diferenciāli šajā punktā.
un noteikt tās diferenciāli šajā punktā.
- Izmantojot funkcijas diferenciāli, izskaitļot
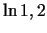 .
.
- Sniegt funkcijas
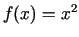 diferenciāļa punktā
diferenciāļa punktā
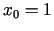 ģeometrisko interpretāciju.
ģeometrisko interpretāciju.
- Pierādīt 1.6. teorēmu.
- Izmantojot diferencēšanas likumus, noteikt šādu funkciju atvasinājumus:
-
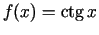 ;
;
-
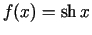 ;
;
-
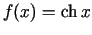 ;
;
-
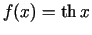 ;
;
-
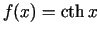 .
.
- Pierādīt, ka
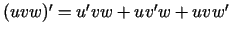 .
.
- Pierādīt, ka
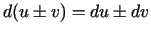 ;
;
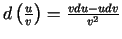 .
.
- Izmantojot apvērstas funkcijas atvasināšanas
formulu, noteikt šādu funkciju atvasinājumus:
-
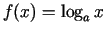 ;
;
-
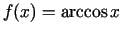 ;
;
-
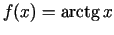 ;
;
-
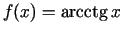 .
.
- Sastādīt elementāro pamatfunkciju atvasinājumu
tabulu pēc starpargumenta
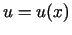 .
.
- Atvasināt šādas funkcijas:
-
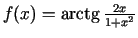 ;
;
-
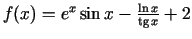 ;
;
-
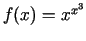 ;
;
-
![$ f(x)=\frac{(x+1)(2x-1)\sqrt{3x+2}}{\sqrt[3]{x}}$](img412.gif) .
.
- Noteikt šādu funkciju
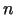 -tās kārtas
atvasinājumus:
-tās kārtas
atvasinājumus:
-
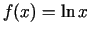 ;
;
-
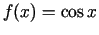 ;
;
-
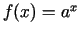 ;
;
-
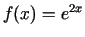 ;
;
-
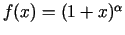 ;
;
-
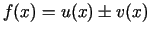 ;
;
-
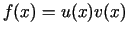 .
.
- Noteikt materiālā punkta ātrumu un
paātrinājumu laika momentā
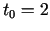 , ja kustības likums ir
, ja kustības likums ir
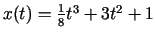 .
.
- Izmantojot definīciju vai aprēķināšanas
formulas, noteikt funkcijas
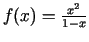 otrās kārtas
diferenciāli un izskaitļot to punktā
otrās kārtas
diferenciāli un izskaitļot to punktā 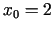 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2. DIFERENCIĀLRĒĶINU PAMATTEORĒMAS
Augstāk: 1. DIFERENCĒJAMAS FUNKCIJAS
Iepriekšējais: 1.9. Jautājumi
2002-01-21
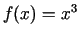 punktā
punktā 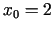 ;
;
![$ f(x)=\sqrt[3]{x}$](img77.gif) punktā
punktā 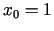 ;
;
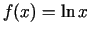 punktā
punktā  ;
;
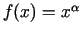 ;
;
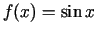 ;
;
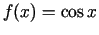 ;
;
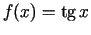 ;
;
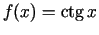 ;
;
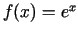 ;
;
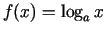 .
.
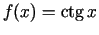 ;
;
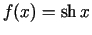 ;
;
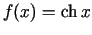 ;
;
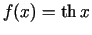 ;
;
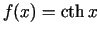 .
.
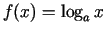 ;
;
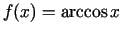 ;
;
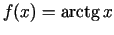 ;
;
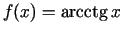 .
.
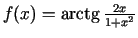 ;
;
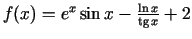 ;
;
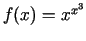 ;
;
![$ f(x)=\frac{(x+1)(2x-1)\sqrt{3x+2}}{\sqrt[3]{x}}$](img412.gif) .
.
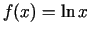 ;
;
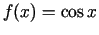 ;
;
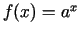 ;
;
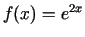 ;
;
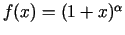 ;
;
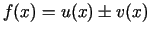 ;
;
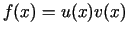 .
.