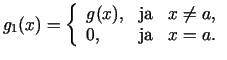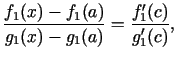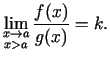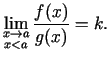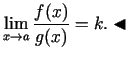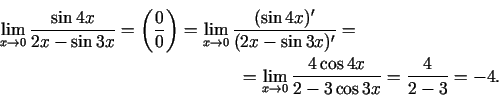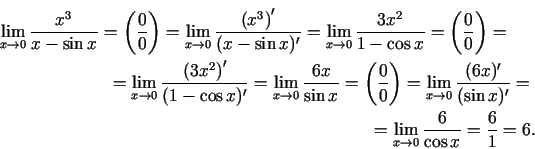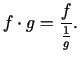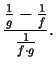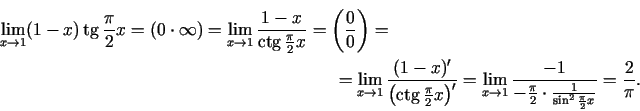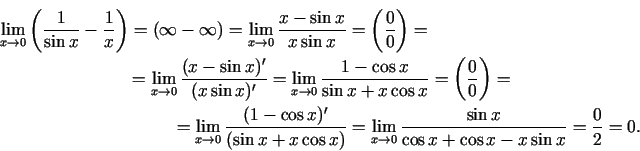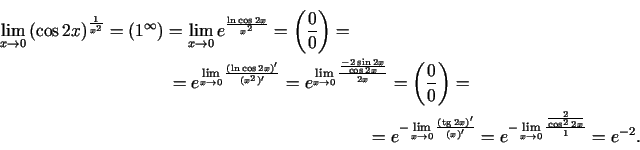Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.6. Teilora formula
Augstāk: 2. DIFERENCIĀLRĒĶINU PAMATTEORĒMAS
Iepriekšējais: 2.4. Košī teorēma (Teorēma par funkciju
2.5. teorēma. Ja funkcijas 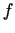 un
un 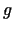 ir definētas un diferencējamas punkta
ir definētas un diferencējamas punkta
 apkārtnē, izņemot varbūt šo punktu, pie tam
apkārtnē, izņemot varbūt šo punktu, pie tam
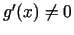 ,
,
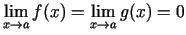 vai
vai
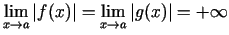 ; eksistē
; eksistē
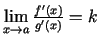 , tad attiecībai
, tad attiecībai
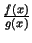 eksistē robeža, kad
eksistē robeža, kad
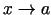 , kas arī ir vienāda ar
, kas arī ir vienāda ar 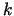 .
.
 Teorēmu pierādīsim tikai nenoteiktībai
Teorēmu pierādīsim tikai nenoteiktībai
 . Punkta
. Punkta 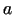 apkārtnē uzdosim šādas divas funkcijas
apkārtnē uzdosim šādas divas funkcijas
un
Funkcijas 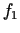 un
un 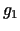 ir nepārtrauktas punktā
ir nepārtrauktas punktā 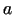 un tā
apkārtnē. Izvēlēsimies patvaļīgu
un tā
apkārtnē. Izvēlēsimies patvaļīgu 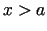 no punkta
no punkta 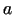 apkārtnes.
Funkcijas
apkārtnes.
Funkcijas 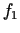 un
un 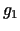 intervālā
intervālā ![$ [a;x]$](img508.gif) apmierina Košī teorēmas
nosacījumus, tāpēc
apmierina Košī teorēmas
nosacījumus, tāpēc
kur 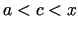 .
.
Ņemot vērā to, kā ir uzdotas funkcijas 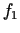 un
un 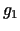 , iegūsim
, iegūsim
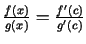 , kur
, kur 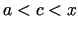 .
.
Tā kā
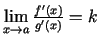 , tad šīs
vienādības labajai, tātad arī kreisajai pusei eksistē robeža no
labās puses punktā
, tad šīs
vienādības labajai, tātad arī kreisajai pusei eksistē robeža no
labās puses punktā 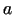 , pie tam
, pie tam
(Acīmredzot, ja
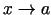 , tad arī
, tad arī
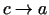 ).
).
Ja tagad izvēlētos patvaļīgu 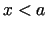 no punkta
no punkta 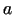 apkārtnes un
rīkotos analogi, tad iegūtu:
apkārtnes un
rīkotos analogi, tad iegūtu:
Tātad eksistē
-
2.5. piezīme.
- Izmantojot iegūtos rezultātus, ar
substitūciju
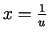 var pierādīt, ka teorēma ir pareiza
arī tad, kad
var pierādīt, ka teorēma ir pareiza
arī tad, kad
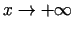 vai
vai
 .
.
No teorēmas izriet šāds paņēmiens
(Lopitāla2.4kārtula) nenoteiktību
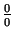 vai
vai
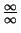 atklāšanai: lai aprēķinātu
atklāšanai: lai aprēķinātu
 , kad skaitītājs un
saucējs reizē tiecas uz nulli vai bezgalību, ir atsevišķi
jāatvasina skaitītājs un saucējs un jāaprēķina
atvasinājumu attiecības robeža, kad
, kad skaitītājs un
saucējs reizē tiecas uz nulli vai bezgalību, ir atsevišķi
jāatvasina skaitītājs un saucējs un jāaprēķina
atvasinājumu attiecības robeža, kad
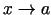 . Ja
iegūtā robeža atkal ir nenoteiktība
. Ja
iegūtā robeža atkal ir nenoteiktība
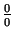 vai
vai
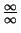 , tad paņēmienu drīkst atkārtot.
, tad paņēmienu drīkst atkārtot.
-
2.1. piemērs.
- Aprēķināt
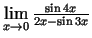 .
.
Lietojot Lopitāla kārtulu vienu reizi, iegūsim
-
2.2. piemērs.
- Aprēķināt
 .
.
Lietojot Lopitāla kārtulu trīs reizes, iegūsim
-
2.3. piemērs.
- Aprēķināt
 (n - naturāls skaitlis).
(n - naturāls skaitlis).
Lietojot Lopitāla kārtulu 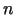 reizes, iegūsim
reizes, iegūsim
Lai, izmantojot Lopitāla kārtulu, atklātu nenoteiktības
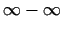 ,
,
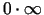 ,
,  ,
,
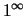 ,
,
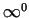 , tās vispirms jāreducē uz nenoteiktībām
, tās vispirms jāreducē uz nenoteiktībām
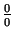 vai
vai
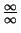 .
.
Nenoteiktību
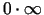 var reducēt uz nenoteiktību
var reducēt uz nenoteiktību
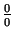 šādi:
šādi:
Nenoteiktības
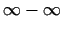 gadījumā
gadījumā 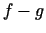 pārveido šādi:
pārveido šādi:
Iegūst nenoteiktību
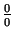 .
.
Pārējās nenoteiktības ( ,
,
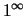 ,
,
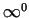 ) reducē
uz nenoteiktību
) reducē
uz nenoteiktību
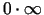 , uzrakstot
, uzrakstot 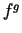 izskatā
izskatā
 .
.
-
2.4. piemērs.
- Aprēķināt
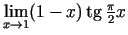 .
.
-
2.5. piemērs.
- Aprēķināt
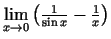 .
.
-
2.6. piemērs.
- Aprēķināt
 .
.
-
2.6. piezīme.
- Saskaņā ar Lopitāla kārtulu, ja
eksistē funkciju atvasinājumu attiecības robeža, tad
eksistē arī šo funkciju attiecības robeža. Turpretī, ja
atvasinājumu attiecības robeža neeksistē, tad tas vēl
nenozīmē, ka neeksistē funkciju attiecības robeža.
Piemēram,
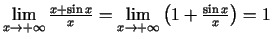 eksistē, lai gan atvasinājumu attiecības
eksistē, lai gan atvasinājumu attiecības
 robeža, kad
robeža, kad
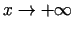 , neeksistē.
, neeksistē.



 Matemātika
DU TSC
Matemātika
DU TSC
Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.6. Teilora formula
Augstāk: 2. DIFERENCIĀLRĒĶINU PAMATTEORĒMAS
Iepriekšējais: 2.4. Košī teorēma (Teorēma par funkciju
2002-01-21
![]() un
un ![]() ir definētas un diferencējamas punkta
ir definētas un diferencējamas punkta
![]() apkārtnē, izņemot varbūt šo punktu, pie tam
apkārtnē, izņemot varbūt šo punktu, pie tam
![]() ,
,
![]() vai
vai
![]() ; eksistē
; eksistē
![]() , tad attiecībai
, tad attiecībai
![]() eksistē robeža, kad
eksistē robeža, kad
![]() , kas arī ir vienāda ar
, kas arī ir vienāda ar ![]() .
.