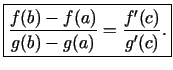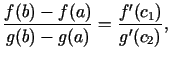Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.5. Lopitāla kārtula
Augstāk: 2. DIFERENCIĀLRĒĶINU PAMATTEORĒMAS
Iepriekšējais: 2.3. Lagranža teorēma
2.4. teorēma. Ja funkcijas  un
un 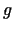 ir nepārtrauktas
slēgtā intervālā
ir nepārtrauktas
slēgtā intervālā ![$ [a;b]$](img437.gif) un diferencējamas šī intervāla iekšējos
punktos, pie tam
un diferencējamas šī intervāla iekšējos
punktos, pie tam
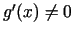 , tad eksistē vismaz viens tāds
intervāla iekšējais punkts
, tad eksistē vismaz viens tāds
intervāla iekšējais punkts 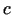 , kurā
, kurā
Pierādīt patstāvīgi.2.3
-
2.4. piezīme.
-

- Pierādot Košī teorēmu, starpības
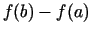 un
un 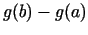 nedrīkst pārveidot saskaņā ar Lagranža
formulu, jo, tā rīkojoties, iegūtu
nedrīkst pārveidot saskaņā ar Lagranža
formulu, jo, tā rīkojoties, iegūtu
kur
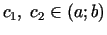 .
.
- Ja
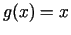 , tad kā Košī teorēmas
secinājums ir Lagranža teorēma.
, tad kā Košī teorēmas
secinājums ir Lagranža teorēma.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.5. Lopitāla kārtula
Augstāk: 2. DIFERENCIĀLRĒĶINU PAMATTEORĒMAS
Iepriekšējais: 2.3. Lagranža teorēma
2002-01-21
![]() un
un ![]() ir nepārtrauktas
slēgtā intervālā
ir nepārtrauktas
slēgtā intervālā ![]() un diferencējamas šī intervāla iekšējos
punktos, pie tam
un diferencējamas šī intervāla iekšējos
punktos, pie tam
![]() , tad eksistē vismaz viens tāds
intervāla iekšējais punkts
, tad eksistē vismaz viens tāds
intervāla iekšējais punkts ![]() , kurā
, kurā